23 Objects and Classes
This book, when initially introducing Python, mentioned some of the features of the language, such as its emphasis on “one best way” and readable code. Python also provides quite a bit of built-in functionality through importable modules such as sys, re, and subprocess.
Python provides another advantage: it is naturally “object oriented,” even though we haven’t discussed this point yet. Although there are competing paradigms for the best way to architect programs, the object-oriented paradigm is commonly used for software engineering and large-project management.[1] Even for small programs, though, the basic concepts of object orientation can make the task of programming easier.
An object, practically speaking, is a segment of memory (RAM) that references both data (referred to by instance variables) of various types and associated functions that can operate on the data.[2] Functions belonging to objects are called methods. Said another way, a method is a function that is associated with an object, and an instance variable is a variable that belongs to an object.
In Python, objects are the data that we have been associating with variables. What the methods are, how they work, and what the data are (e.g., a list of numbers, dictionary of strings, etc.) are defined by a class: the collection of code that serves as the “blueprint” for objects of that type and how they work.
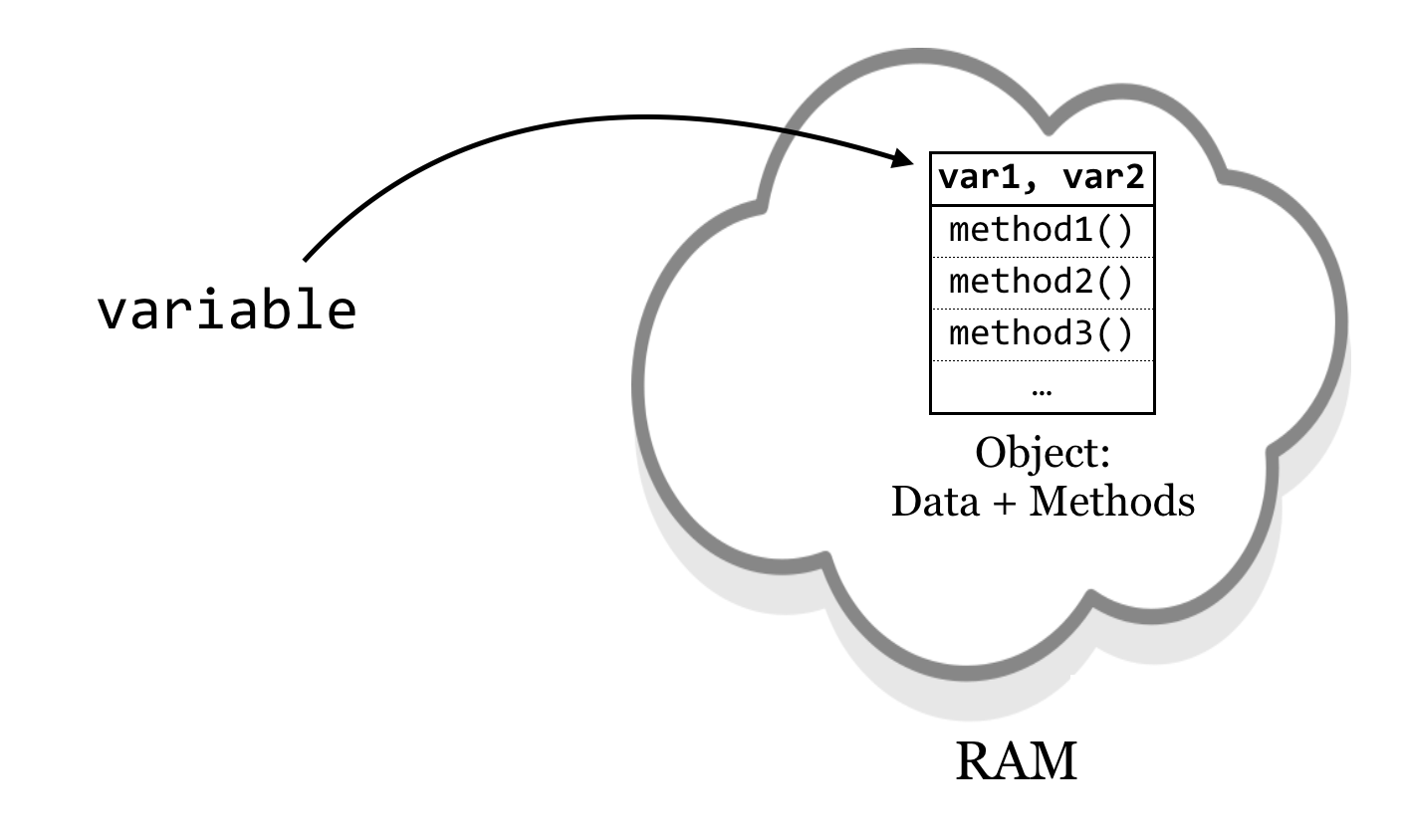
Thus the class (much like the blueprint for a house) defines the structure of objects, but each object’s instance variables may refer to different data elements so long as they conform to the defined structure (much like how different families may live in houses built from the same blueprint). In Python, each piece of data we routinely encounter constitutes an object. Each data type we’ve dealt with so far (lists, strings, dictionaries, and so on) has a class definition—a blueprint—that defines it. For example, lists have data (numbers, strings, or any other type) and methods such as .sort() and .append().

In a sense, calling object methods makes a request of the object: nums_list.sort() might be interpreted as “object referred to by nums_list, please run your sort() method.” Upon receiving this message, the object will reorder its data.[3]
Creating New Classes
Definitions for Python classes are just blocks of code, indicated by an additional level of indentation (like function blocks, if-statement blocks, and loop blocks). Each class definition requires three things, two of which we are already familiar with:
- Methods (functions) that belong to objects of the class.
- Instance variables referring to data.
- A special method called a constructor. This method will be called automatically whenever a new object of the class is created, and must have the name
__init__.
One peculiarity of Python is that each method of an object must take as its first argument a parameter called self,[4] which we use to access the instance variables. Let’s start by defining a class, Gene (class names traditionally begin with a capital letter): each Gene object will have (1) an id (string) and (2) a sequence (also a string). When creating a Gene object, we should define its id and sequence by passing them as parameters to the __init__ method.
Outside of the block defining the class, we can make use of it to create and interact with Gene objects.

(Normally we don’t include print() calls in the constructor; we’re doing so here just to clarify the object creation process.) Executing the above:

Note that even though each method (including the constructor) takes as its first parameter self, we don’t specify this parameter when calling methods for the objects. (For example, .print_id() takes a self parameter that we don’t specify when calling it.) It’s quite common to forget to include this “implicit” self parameter; if you do, you’ll get an error like TypeError: print_id() takes no arguments (1 given), because the number of parameters taken by the method doesn’t match the number given when called. Also, any parameters sent to the creation function (Gene("AY342", "CATTGAC")) are passed on to the constructor (__init__(self, creationid, creationseq)).
What is self? The self parameter is a variable that is given to the method so that the object can refer to “itself.” Much like other people might refer to you by your name, you might refer to yourself as “self,” as in “self: remember to resubmit that manuscript tomorrow.”
Interestingly, in some sense, the methods defined for classes are breaking the first rule of functions: they are accessing variables that aren’t passed in as parameters! This is actually all right. The entire point of objects is that they hold functions and data that the functions can always be assumed to have direct access to.
Let’s continue our example by adding a method that computes the GC content of the self.sequence instance variable. This method needs to be included in the block defining the class; notice that a method belonging to an object can call another method belonging to itself, so we can compute GC content as a pair of methods, much like we did with simple functions:
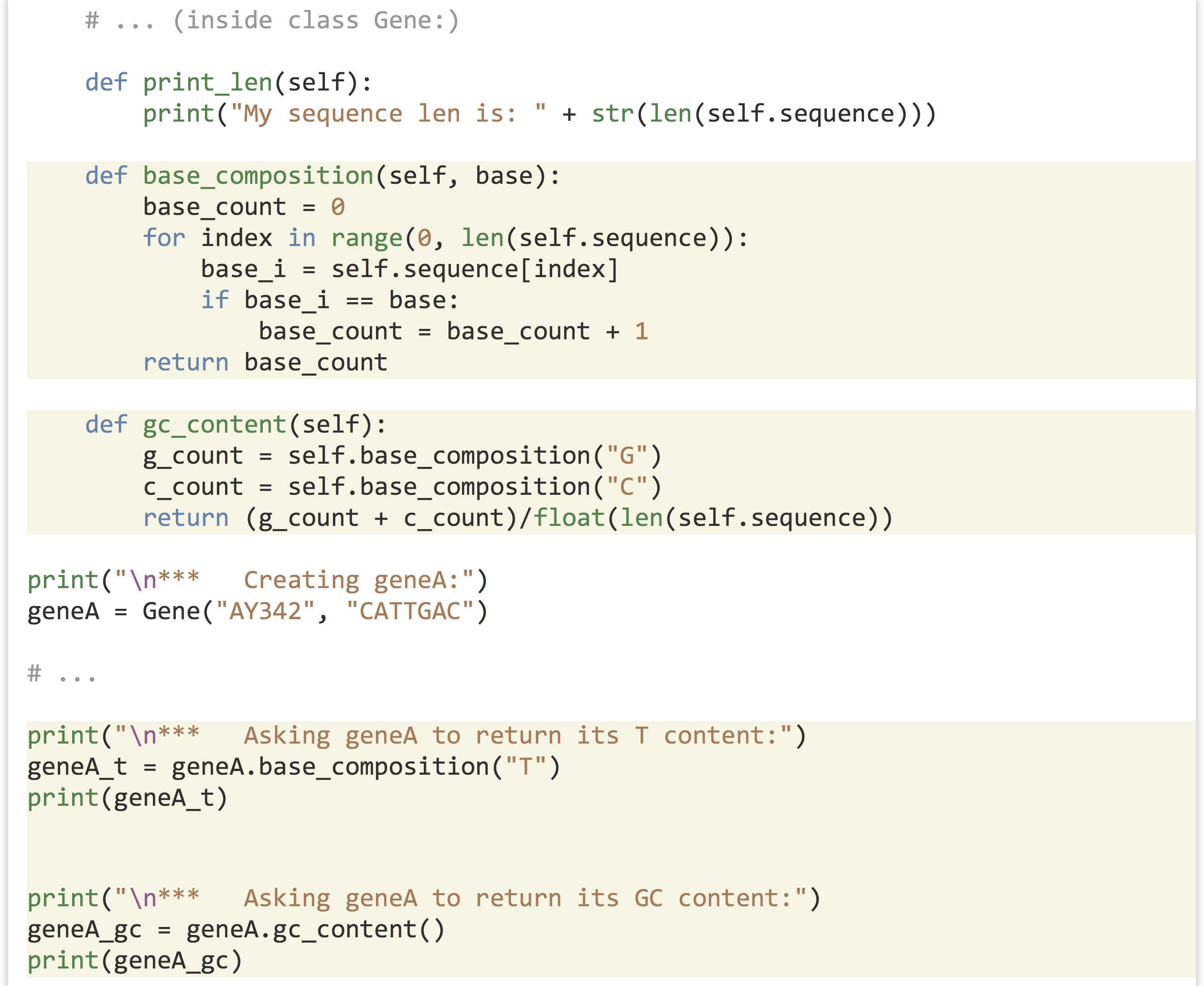
Resulting in the output:

It can also be useful to write methods that let us get and set the instance variables of an object. We might add to our class definition methods to get and set the sequence, for example, by having the methods refer to the self.seq instance variable.
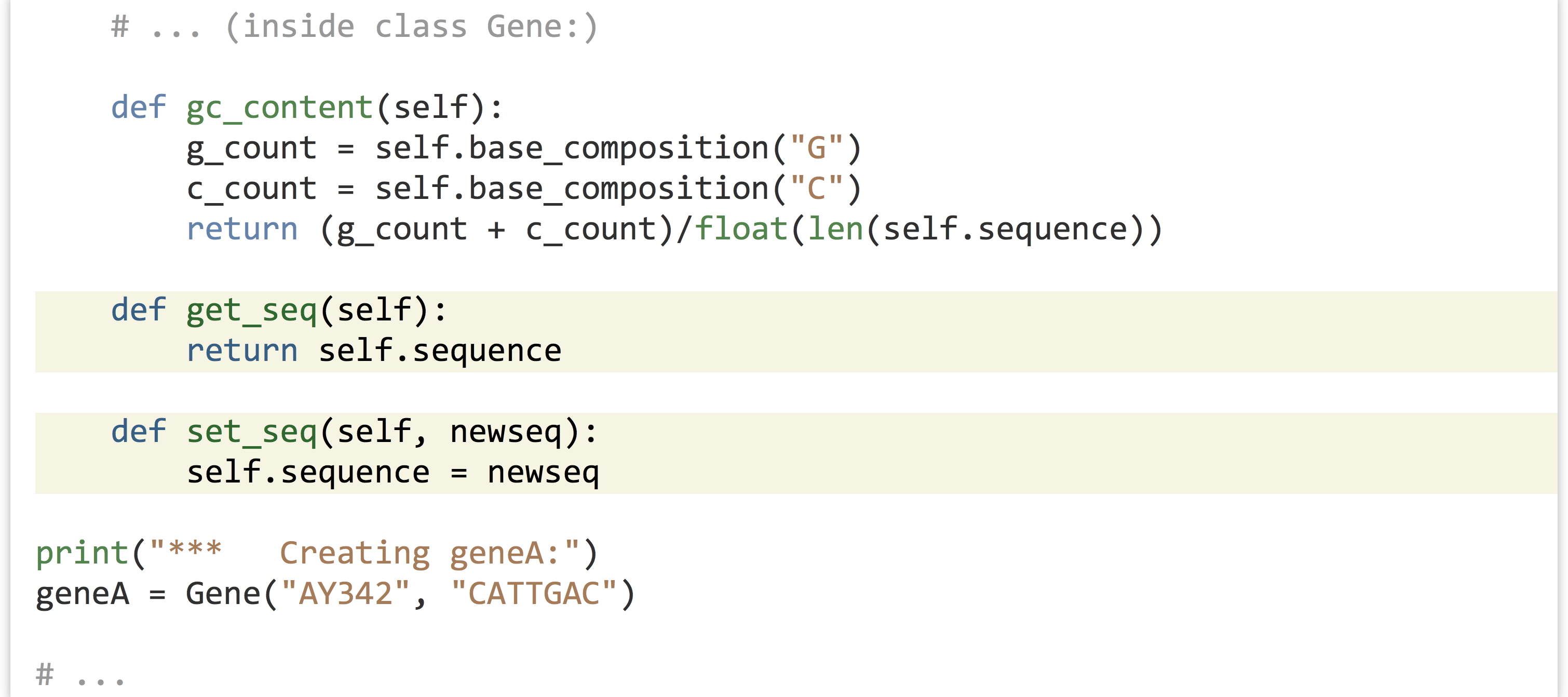
We could make use of this added functionality later in our code with a line like print("gene A's sequence is " + geneA.get_seq()) or geneA.set_seq("ACTAGGGG").
Although methods can return values (as with .base_composition() and .gc_content()) and perform some action that modifies the object (as with .set_seq()), the principle of command-query separation states that they shouldn’t do both unless it is absolutely necessary.
Is it possible for us to modify the instance variables of an object directly? It makes sense that we can; because the gene object’s name for itself is self and sets its sequence via self.sequence, we should be able to set the gene object’s sequence using our name for it, geneA. In fact, geneA.sequence = "ACTAGGGG" would have the same result as calling geneA.set_seq("ACTAGGGG"), as defined above.
So why might we want to use “getter” and “setter” methods as opposed to directly modifying or reading an object’s instance variables? The difference is related a bit to politeness—if not to the object itself, then to whomever wrote the code for the class. By using methods, we are requesting that the object change its sequence data, whereas directly setting instance variables just reaches in and changes it—which is a bit like performing open-heart surgery without the patient’s permission!
This is a subtle distinction, but it’s considered serious business to many programmers. To see why, suppose that there are many methods that won’t work at all on RNA sequences, so we must make sure that the sequence instance variable never has any U characters in it. In this case, we could have the .set_seq() method decide whether or not to accept the sequence:

Python has an assert statement for this sort of error checking. Like a function, it takes two parameters, but unlike a function, parentheses are not allowed.

When using an assert, if the check doesn’t evaluate to True, then the program will stop and report the specified error. The complete code for this example can be found in the file gene_class.py.
Using methods when working with objects is about encapsulation and letting the objects do as much work as possible. That way, they can ensure correct results so that you (or whomever you are sharing code with, which might be “future you”) don’t have to. Objects can have any number of instance variables, and the methods may access and modify them, but it’s a good idea to ensure that all instance variables are left in a coherent state for a given object. For example, if a Gene object has an instance variable for the sequence, and another holding its GC content, then the GC content should be updated whenever the sequence is. Even better is to compute such quantities as needed, like we did above.[5]
The steps for writing a class definition are as follows:
- Decide what concept or entity the objects of that class will represent, as well as what data (instance variables) and methods (functions) they will have.
- Create a constructor method and have it initialize all of the instance variables, either with parameters passed into the constructor, or as empty (e.g., something like
self.id = ""orself.go_terms = list()). Although instance variables can be created by any method, having them all initialized in the constructor provides a quick visual reference to refer to when coding. - Write methods that set or get the instance variables, compute calculations, call other methods or functions, and so on. Don’t forget the
selfparameter!
Exercises
- Create a program
objects_test.pythat defines and uses a class. The class can be anything you want, but it should have at least two methods (other than the constructor) and at least two instance variables. One of the methods should be an “action” that you can ask an object of that class to perform, and the other should return an “answer.”Instantiate your class into at least two objects, and try your methods on them.
- Once defined, classes (and objects of those types) can be used anywhere, including other class definitions. Write two class definitions, one of which contains multiple instances of the other. For example, instance variables in a
Houseobject could refer to several differentRoomobjects. (For a more biologically inspired example, aGeneobject could have aself.exonsthat contains a list ofExonobjects.)The example below illustrates this more thoroughly, but having some practice first will be beneficial.
- If classes implement some special methods, then we can compare objects of those types with
==,<, and the other comparison operators.When comparing two
Geneobjects, for example, we might say that they are equal if their sequences are equal, andgeneAis less thangeneBifgeneA.seq < geneB.seq. Thus we can add a special method__eq__(), which, given the usualselfand a reference to another object of the same type calledother, returnsTrueif we’d consider the two equal andFalseotherwise: We can also implement an
We can also implement an __lt__()method for “less than”: With these, Python can work out how to compare
With these, Python can work out how to compare Geneobjects with<and==. The other comparisons can be enabled by defining__le__()(for<=),__gt__()(for>),__ge__()(for>=) and__ne__()(for!=). Finally, if we have a list of
Finally, if we have a list of Geneobjectsgenes_listwhich define these comparators, then Python can sort according to our comparison criteria withgenes_list.sort()andsorted(genes_list).Explore these concepts by defining your own ordered data type, implementing
__eq__(),__lt__(), and the other comparison methods. Compare two objects of those types with the standard comparison operators, and sort a list of them. You might also try implementing a__repr__()method, which should return a string representing the object, enablingprint()(as inprint(geneA)).
Counting SNPs
As it turns out, multiple classes can be defined that interact with each other: instance variables of a custom class may refer to custom object types. Consider the file trio.subset.vcf, a VCF (variant call format) file for describing single-nucleotide polymorphisms (SNPs, pronounced “snips”) across individuals in a group or population. In this case, the file represents a random sampling of SNPs from three people—a mother, a father, and their daughter—compared to the reference human genome.[6]
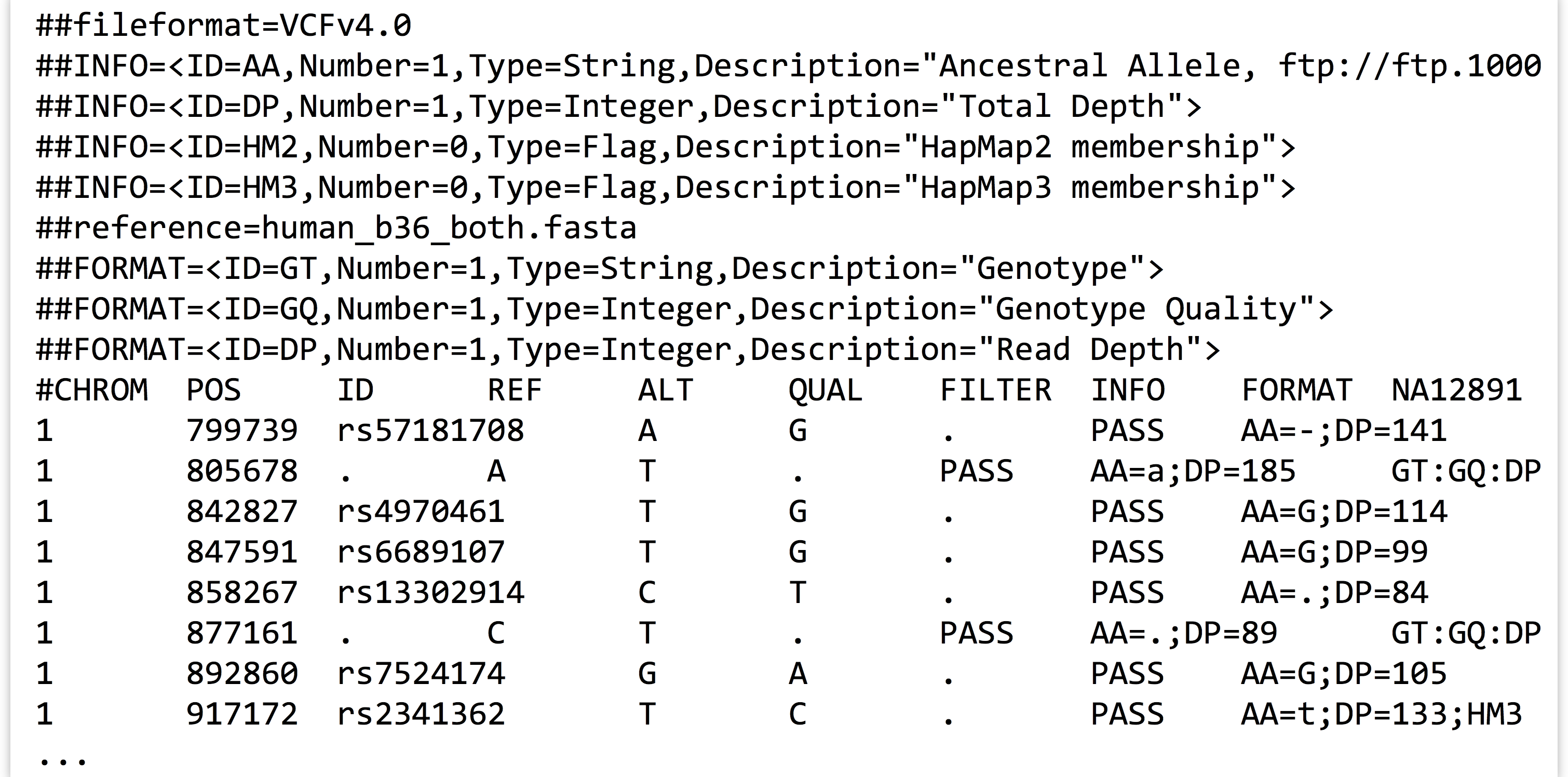
This file contains a variety of information, including header lines starting with # describing some of the coding found in the file. Columns 1, 2, 3, 4, and 5 represent the chromosome number of the SNP, the SNP’s position on the chromosome, the ID of the SNP (if it has previously been described in human populations), the base present in the reference at that position, and an alternative base found in one of the three family members, respectively. Other columns describe various information; this file follows the “VCF 4.0” format, which is described in more detail at http://www.1000genomes.org/node/101. Some columns contain a . entry, which indicates that the information isn’t present; in the case of the ID column, these represent novel polymorphisms identified in this trio.
For this example, we are interested in the first five columns, and the main questions are:
- How many transitions (A vs. G or C vs. T) are there within the data for each chromosome?
- How many transversions (anything else) are there within the data for each chromosome?
We may in the future have other questions about transitions and transversions on a per-chromosome basis. To answer the questions above, and to prepare for future ones, we’ll start by defining some classes to represent these various entities. This example will prove to be a bit longer than others we’ve studied, partially because it allows us to illustrate answering multiple questions using the same codebase if we do some extra work up front, but also because object-oriented designs tend to result in significantly more code (a common criticism of using classes and objects).
SNP Class
A SNP object will hold relevant information about a single nonheader line in the VCF file. Instance variables would include the reference allele (a one-character string, e.g., "A"), the alternative allele (a one-character string, e.g., "G"), the name of the chromosome on which it exists (a string, e.g., "1"), the reference position (an integer, e.g., 799739), and the ID of the SNP (e.g., "rs57181708" or "."). Because we’ll be parsing lines one at a time, all of this information can be provided in the constructor.
SNP objects should be able to answer questions: .is_transition() should return True if the SNP is a transition and False otherwise by looking at the two allele instance variables. Similarly, .is_transversion() should return True if the SNP is a transversion and False otherwise.
Chromosome Class
A Chromosome object will hold data for an individual chromosome, including the chromosome name (a string, e.g., "1"), and all of the SNP objects that are located on that chromosome. We could store the SNP objects in a list, but we could also consider storing them in a dictionary, which maps SNP locations (integers) to the SNP objects. Then we can not only gain access to the list of SNPs (using the dictionary’s .values() method) or the list of locations (using the dictionary’s .keys() method), but also, given any location, we can get access to the SNP at that location. (We can even use .has_key() to determine whether a SNP exists at a given location.)

The chromosome constructor will initialize the name of the chromosome as self.chrname, but the snps dictionary will start as empty.
A Chromosome object should be able to answer questions as well: .count_transitions() should tell us the number of transition SNPs, and .count_transversions() should return the number of transversion SNPs. We’re also going to need some way to add a SNP object to a chromosome’s SNP dictionary because it starts empty. We’ll accomplish this with an .add_snp() method, which will take all of the information for a SNP, create the new SNP object, and add it to the dictionary. If a SNP already exists at that location, an error should occur, because our program shouldn’t accept VCF files that have multiple rows with the same position for the same chromosome.
For overall strategy, once we have our classes defined (and debugged), the “executable” portion of our program will be fairly simple: we’ll need to keep a collection of Chromosome objects that we can interact with to add SNPs, and at the end we’ll just loop through these and ask each how many transitions and transversions it has. It makes sense to keep these Chromosome objects in a dictionary as well, with the keys being the chromosome names (strings) and the values being the Chromosome objects. We’ll call this dictionary chrnames_to_chrs.
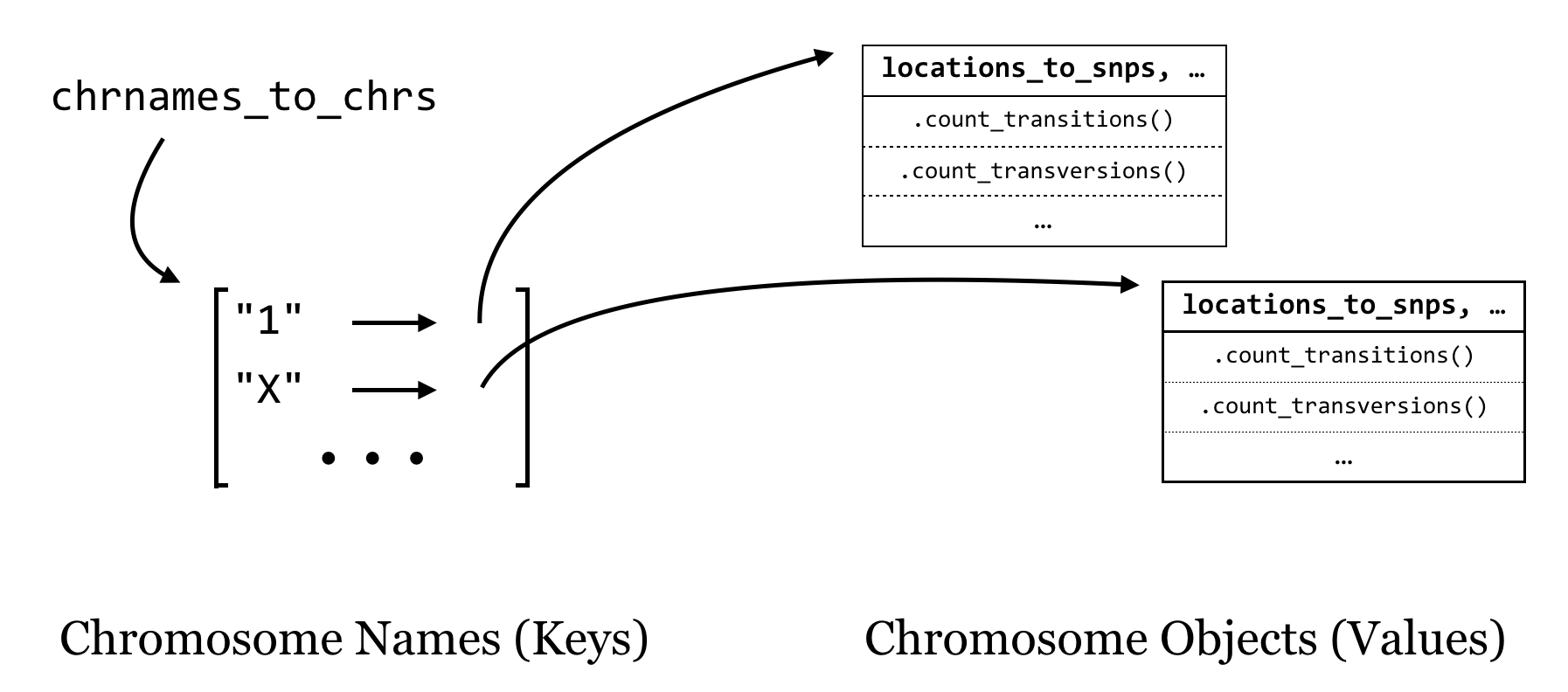
As we loop through each line of input (reading a file name given in sys.argv[1]), we’ll split it apart and check whether the chromosome name is in the dictionary with .has_key(). If so, we’ll ask the object in that slot to add a SNP with .add_snp(). If not, then we’ll need to first create a new Chromosome object, ask it to .add_snp(), and finally add it to the dictionary. Of course, all of this should happen only for nonheader lines.
We’ll start with the SNP class, and then the Chromosome class. Although it is difficult to show here, it’s a good idea to work on and debug each method in turn (with occasional print() statements), starting with the constructors. Because a SNP is only a SNP if the reference and alternative allele differ, we’ll assert this condition in the constructor so an error is produced if we ever try to create a nonpolymorphic SNP (which wouldn’t actually be a SNP at all).

Note the shortcut that we took in the above code for the .is_transversion() method, which calls the .is_transition() method and returns the opposite answer. This sort of “shortcut” coding has its benefits and downsides. One benefit is that we can reuse methods rather than copying and pasting to produce many similar chunks of code, reducing the potential surface area for bugs to occur. A downside is that we have to be more careful—in this case, we’ve had to ensure that the alleles differ (via the assert in the constructor), so a SNP must be either a transition or transversion. (Is this actually true? What if someone were to attempt to create a SNP object with non-DNA characters? It’s always wise to consider ways code could be inadvertently misused.)
The above shows the start of the script and the SNP class; code like this could be tested with just a few lines:

Although we won’t ultimately leave these testing lines in, they provide a good sanity check for the code. If these checks were wrapped in a function that could be called whenever we make changes to the code, we would have what is known as a unit test, or a collection of code (often one or more functions), with the specific purpose of testing functionality of other code for correctness.[7] These can be especially useful as code changes over time.
Let’s continue on with the Chromosome class. Note that the .add_snp() method contains assertions that the SNP location is not a duplicate and that the chromosome name for the new SNP matches the chromosome’s self.chrname.
Now we can write the methods for .count_transitions() and .count_transversions(). Because we’ve ensured that each SNP object is either a transition or a transversion, and no locations are duplicated within a chromosome, the .count_transversions() method can make direct use of the .count_transitions() method and the total number of SNPs stored via len(self.locations_to_snps). (Alternatively, we could make a count_transversions() that operates similarly to count_transitions() by looping over all the SNP objects.)
The corresponding test code is below. Here we are using assert statements, but we could also use lines like print(chr1.count_transitions()) and ensure the output is as expected.

With the class definitions created and debugged, we can write the “executable” part of the program, concerned with parsing the input file (from a filename given in sys.argv[1]) and printing the results. First, the portion of code that checks whether the user has given a file name (and produces some help text if not) and reads the data in. Again, we are storing a collection of Chromosome objects in a chrnames_to_chrs dictionary. For each VCF line, we determine whether a Chromosome with that name already exists: if so, we ask that object to .add_snp(). If not, we create a new Chromosome object, ask it to .add_snp(), and add it to the dictionary.
In the chr_obj = chrnames_to_chrs[chrname] line above, we are defining a variable referring to the Chromosome object in the dictionary, and after that we are asking that object to add the SNP with .add_snp(). We could have combined these two with syntax like chrnames_to_chrs[chrname].add_snp().
Finally, a small block of code prints out the results by looping over the keys in the dictionary, accessing each Chromosome object and asking it the number of transitions and transversions:

We’ll have to remove or comment out the testing code (particularly the tests we expected to fail) to see the results. But once we do that, we can run the program (called snps_ex.py).
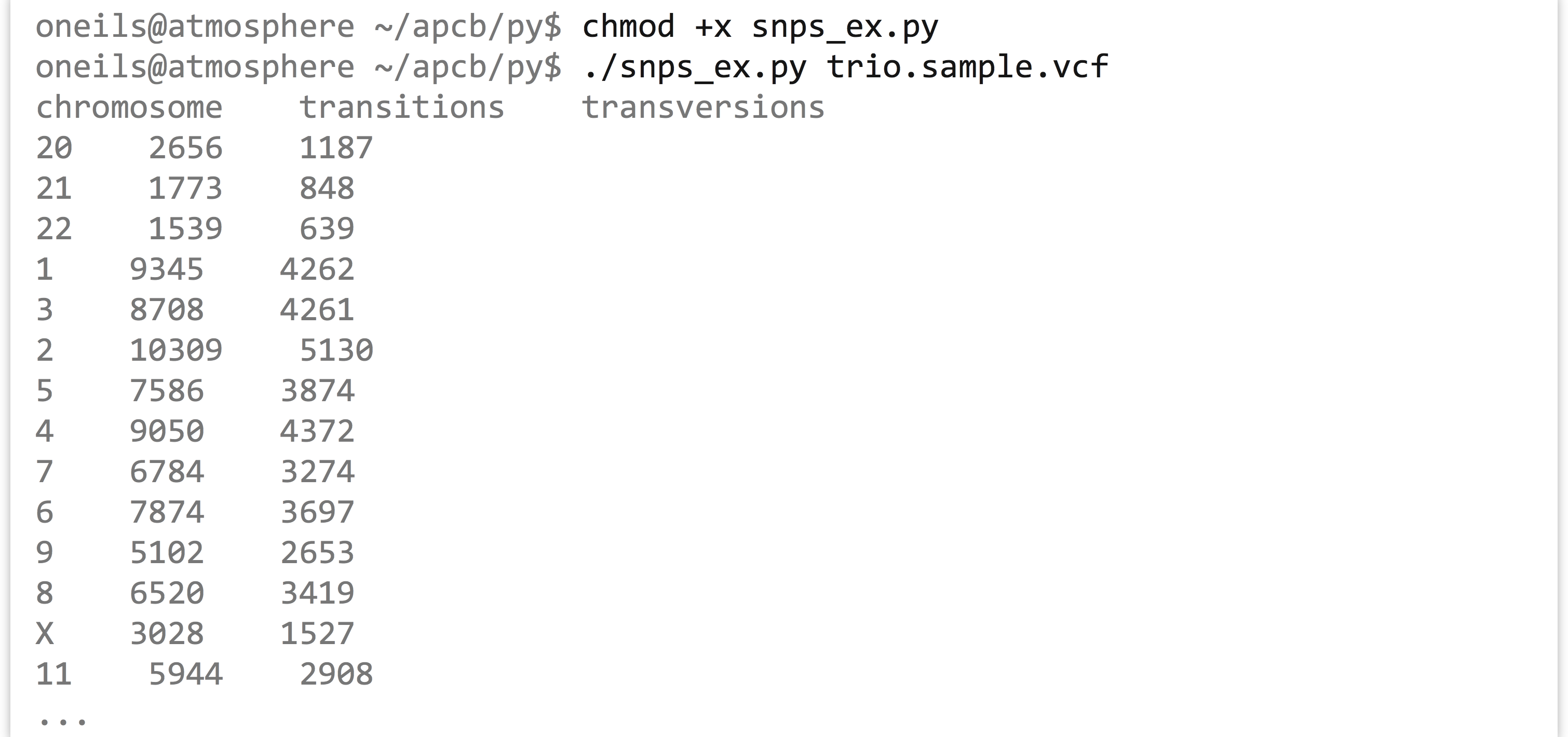
What we’ve created here is no small thing, with nearly 150 lines of code! And yet each piece of code is encapsulated in some way; even the long for-loop represents the code to parse the input file and populate the chrnames_to_chrs dictionary. By clearly naming our variables, methods, and classes we can quickly see what each entity does. We can reason about this program without too much difficulty at the highest level of abstraction but also delve down to understand each piece individually. As a benefit, we can easily reuse or adapt this code in a powerful way by adding or modifying methods.
An Extension: Searching for SNP-Dense Regions
Counting transitions and transversions on a per-chromosome basis for this VCF file could have been accomplished without defining classes and objects. But one of the advantages of spending some time organizing the code up front is that we can more easily answer related questions about the same data.
Suppose that, having determined the number of transitions and transversions per chromosome, we’re now interested in determining the most SNP-dense region of each chromosome. There are a number of ways we could define SNP density, but we’ll choose an easy one: given a region from positions l to m, the density is the number of SNPs occurring within l and m divided by the size of the region, m – l + 1, times 1,000 (for SNPs per 1,000 base pairs).
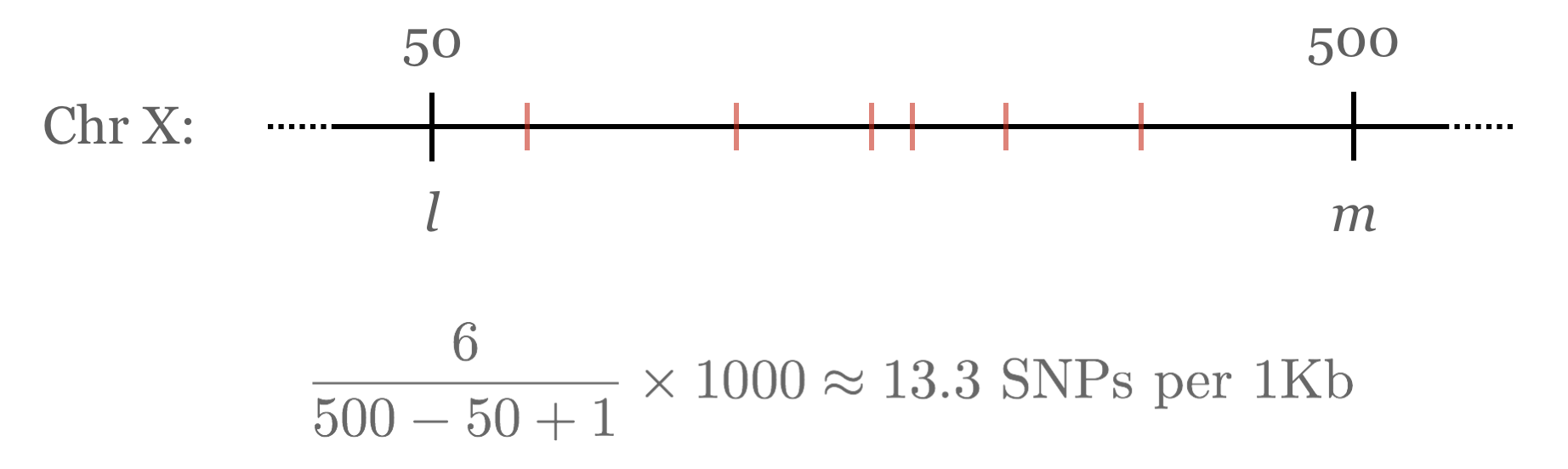
For a Chromosome object to be able to tell us the highest-density region, it will need to be able to compute the density for any given region by counting the SNPs in that region. We can start by adding to the chromosome class a method that computes the SNP density between two positions l and m.

After debugging this method and ensuring it works, we can write a method that finds the highest-density region. But how should we define our regions? Let’s say we want to consider regions of 100,000 bases. Then we might consider bases 1 to 100,000 to be a region, 100,001 to 200,000 to be a region, and so on, up until the start of the region considered is past the last SNP location. We can accomplish this with a while-loop. The strategy will be to keep information on the densest region found so far (including its density as well as start and end location), and update this answer as needed in the loop.[8]

In the above, we needed to access the position of the last SNP on the chromosome (so that the code could stop considering regions beyond the last SNP). Rather than write that code directly in the method, we decided that should be its own method, and marked it with a “todo” comment. So, we need to add this method as well:

In the code that prints the results, we can add the new call to .max_density(100000) for each chromosome, and print the relevant information.
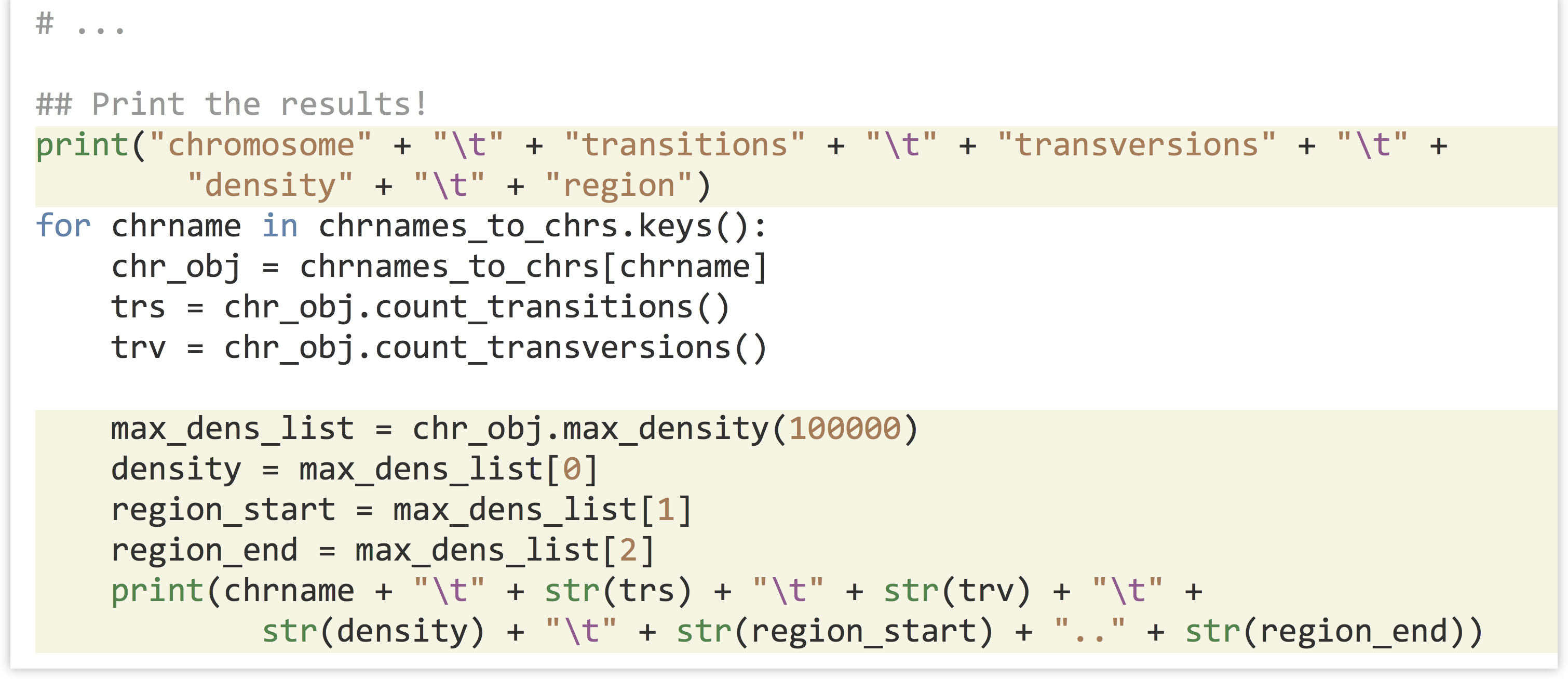
Let’s call our new snps_ex_density.py (piping the result through column -t to more easily see the tab-separated column layout):

Again, none of the individual methods or sections of code are particularly long or complex, yet together they represent a rather sophisticated analysis program.
Summary
Perhaps you find these examples using classes and objects for problem solving to be elegant, or perhaps not. Some programmers think that this sort of organization results in overly verbose and complex code. It is certainly easy to get too ambitious with the idea of classes and objects. Creating custom classes for every little thing risks confusion and needless hassle. In the end, it is up to each programmer to decide what level of encapsulation is right for the project; for most people, good separation of concepts by using classes is an art form that requires practice.
When should you consider creating a class?
- When you have many different types of data relating to the same concept, and you’d like to keep them organized into single objects as instance variables.
- When you have many different functions related to the same concept, and you’d like to keep them organized into single objects as methods.
- When you have a concept that is simple now, but you suspect might increase in complexity in the future as you add to it. Like functions, classes enable code to be reused, and it is easy to add new methods and instance variables to classes when needed.
Inheritance and Polymorphism
Despite this discussion of objects, there are some unique features of the object-oriented paradigm that we haven’t covered but are sometimes considered integral to the topic. In particular, most object-oriented languages (Python included) support inheritance and polymorphism for objects and classes.
Inheritance is the idea that some types of classes may be represented as special cases of other types of classes. Consider a class defining a Sequence, which might have instance variables for self.seq and self.id. Sequences might be able to report their length, and so might have a .length_bp() method, returning len(self.seq). There may also be many other operations a generic Sequence could support, like .get_id(). Now, suppose we wanted to implement an OpenReadingFrame class; it too should have a self.id and a self.seq and be able to report its .length_bp(). Because an object of this type would represent an open reading frame, it probably should also have a .get_translation() method returning the amino-acid translation of its self.seq. By using inheritance, we can define the OpenReadingFrame class as a type of Sequence class, saving us from having to re-implement .length_bp()—we’d only need to implement the class-specific .get_translation() method and any other methods would be automatically inherited from the Sequence class.

Polymorphism is the idea that inheriting class types don’t have to accept the default methods inherited, and they are free to re-implement (or “override”) specific methods even if their “parent” or “sibling” classes already define them. For example, we might consider another class called AminoAcidSequence that inherits from Sequence, so it too will have a .get_id() and .length_bp(); in this case, though, the inherited .length_bp() would be wrong, because len(self.seq) would be three times too short. So, an AminoAcidSequence could override the .length_bp() method to return 3*len(self.seq). The interesting feature of polymorphism is that given an object like gene_A, we don’t even need to know what “kind” of Sequence object it is: running gene_A.length_bp() will return the right answer if it is any of these three kinds of sequence.

These ideas are considered by many to be the defining points of “object-oriented design,” and they allow programmers to structure their code in hierarchical ways (via inheritance) while allowing interesting patterns of flexibility (via polymorphism). We haven’t covered them in detail here, as making good use of them requires a fair amount of practice. Besides, the simple idea of encapsulating data and functions into objects provides quite a lot of benefit in itself!
Exercises
- Modify the
snps_ex_density.pyscript to output, for each 100,000bp region of each chromosome, the percentage of SNPs that are transitions and the number of SNPs in each window. The output should be a format that looks like so:
 In the section on R programming (chapter 37, “Plotting Data and
In the section on R programming (chapter 37, “Plotting Data and ggplot2”), we’ll discover easy ways to visualize this type of output. - The
randommodule (used withimport random) allows us to make random choices; for example,random.random()returns a random float between0.0and1.0. Therandom.randint(a, b)function returns a random integer betweenaandb(inclusive); for example,random.randint(1, 4)could return1,2,3, or4. There’s also arandom.choice()function; given a list, it returns a single element (at random) from it. So, ifbases = ["A", "C", "T", "G"], thenrandom.choice(bases)will return a single string, either"A","C","T", or"G".Create a program called
pop_sim.py. In this program write aBugclass; a “bug” object will represent an individual organism with a genome, from which a fitness can be calculated. For example, ifa = Bug(), perhapsawill have aself.genomeas a list of 100 random DNA bases (e.g.["G", "T", "A", "G", ...; these should be created in the constructor). You should implement a.get_fitness()method which returns a float computed in some way fromself.genome, for example the number of G or C bases, plus 5 if the genome contains three"A"characters in a row. Bug objects should also have a.mutate_random_base()method, which causes a random element ofself.genometo be set to a random element from["A", "C", "G", "T"]. Finally, implement a.set_base()method, which sets a specific index in the genome to a specific base:a.set_base(3, "T")should setself.genome[3]to"T".Test your program by creating a list of 10
Bugobjects, and in a for-loop, have each run its.mutate_random_base()method and print its new fitness. - Next, create a
Populationclass. Population objects will have a list ofBugobjects (say, 50) calledself.bug_list.This
Populationclass should have a.create_offspring()method, which will: 1) create anew_poplist, 2) for each elementoldbugofself.bug_list: a) create a newBugobjectnewbug, b) and set the genome ofnewbug(one base at a time) to be the same as that ofoldbug, c) callnewbug.mutate_random_base(), and d) addoldbugandnewbugtonew_pop. Finally, this method should 3) setself.bug_poptonew_pop.The
Populationclass will also have a.cull()method; this should reduceself.bug_popto the top 50% of bug objects by fitness. (You might find the exercise above discussing.__lt__()and similar methods useful, as they will allow you to sortself.bug_popby fitness if implemented properly.)Finally, implement a
.get_mean_fitness()method, which should return the average fitness ofself.bug_pop.To test your code, instantiate a
p = Population()object, and in a for-loop: 1) runp.create_offspring(), 2) runp.cull(), and 3) printp.get_mean_fitness(), allowing you to see the evolutionary progress of your simulation. - Modify the simulation program above to explore its dynamics. You could consider adding a
.get_best_individual()method to thePopulationclass, for example, or implement a “mating” scheme whereby offspring genomes are mixes of two parent genomes. You could also try tweaking the.get_fitness()method. This sort of simulation is known as a genetic algorithm, especially when the evolved individuals represent potential solutions to a computational problem.[9]
- Another prominent methodology for programming is the “functional” paradigm, wherein functions are the main focus and data are usually immutable. While Python also supports functional programming, we won’t focus on this topic. On the other hand, the R programming language emphasizes functional programming, so we’ll explore this paradigm in more detail in later chapters. ↵
- This definition is not precise, and in fact intentionally misrepresents how objects are stored in RAM. (In reality, all objects of the same type share a single set of functions/methods.) But this definition will serve us well conceptually. ↵
- Although some have criticized the anthropomorphization of objects this way, it’s perfectly fine—so long as we always say “please!” ↵
- This first parameter doesn’t technically need to be named
self, but it is a widely accepted standard. ↵ - One might ask whether a
Geneobject would ever need to allow its sequence to change at all. One possible reason would be if we were simulating mutations over time; a method like.mutate(0.05)might ask a gene to randomly change 5% of its bases. ↵ - This file was obtained from the 1000 Human Genomes Project at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/pilot_data/release/2010_07/trio/snps/, in the file
CEU.trio.2010_03.genotypes.vcf.gz. After decompressing, we sampled 5% of the SNPs at random withawk '{if($1 ~ "##" || rand() < 0.05) {print $0}}' CEU.trio.2010_03.genotypes.vcf > trio.sample.vcf; see chapter 10, "Rows and Columns" for details. ↵ - Unit tests are often automated; in fact, Python includes a module for building unit tests called
unittest. ↵ - This strategy is not the fastest we could have devised. In order to determine the highest-density region, we have to consider each region, and the computation for each region involves looping over all of the SNP positions (the vast majority of which lie outside the region). More sophisticated algorithms exist that would run much faster, but they are outside the scope of this book. Nevertheless, a slow solution is better than no solution! ↵
- The idea of simulating populations “in silico” is not only quite fun, but has also produced interesting insights into population dynamics. For an example, see Hinton and Nowlan, “How Learning Can Guide Evolution,” Complex Systems 1 (1987): 495–502. Simulation of complex systems using random sampling is commonly known as a Monte Carlo method. For a more fanciful treatment of simulations of natural systems, see Daniel Shiffman, The Nature of Code (author, 2012). The examples there use the graphical language available at http://processing.org, though a Python version is also available at http://py.processing.org. ↵

