32 Character and Categorical Data
Scientific data sets, especially those to be analyzed statistically, commonly contain “categorical” entries. If each row in a data frame represents a single measurement, then one column might represent whether the measured value was from a “male” or “female,” or from the “control” group or “treatment” group. Sometimes these categories, while not numeric, have an intrinsic order, like “low,” “medium,” and “high” dosages.
Sadly, more often than not, these entries are not encoded for easy analysis. Consider the tab-separated file expr_long_coded.txt, where each line represents an (normalized) expression reading for a gene (specified by the ID column) in a given sample group. This experiment tested the effects of a chemical treatment on an agricultural plant species. The sample group encodes information about what genotype was tested (either C6 or L4), the treatment applied to the plants (either control or chemical), the tissue type measured (either A, B, or C for leaf, stem, or root), and numbers for statistical replicates (1, 2, or 3).

Initially, we’ll read the table into a data frame. For this set of data, we’ll likely want to work with the categorical information independently, for example, by extracting only values for the chemical treatment. This would be much easier if the data frame had individual columns for genotype, treatment, tissue, and replicate as opposed to a single, all-encompassing sample column.
A basic installation of R includes a number of functions for working with character vectors, but the stringr package (available via install.packes("stringr") on the interactive console) collects many of these into a set of nicely named functions with common options. For an overview, see help(package = "stringr"), but in this chapter we’ll cover a few of the most important functions from that package.

Splitting and Binding Columns
The str_split_fixed() function from the stringr package operates on each element of a character vector, splitting it into pieces based on a pattern. With this function, we can split each element of the expr_long$sample vector into three pieces based on the pattern "_". The “pattern” could be a regular expression, using the same syntax as used by Python (and similar to that used by sed).

The value returned by the str_split_fixed() function is a matrix: like vectors, matrices can only contain a single data type (in fact, they are vectors with attributes specifying the number of rows and columns), but like data frames they can be accessed with [<row_selector>, <column_selector>] syntax. They may also have row and column names.

Anyway, we’ll likely want to convert the matrix into a data frame using the data.frame() function, and assign some reasonable column names to the result.

At this point, we have a data frame expr_long as well as sample_split_df. These two have the same number of rows in a corresponding order, but with different columns. To get these into a single data frame, we can use the cbind() function, which binds such data frames by their columns, and only works if they contain the same number of rows.

A quick print(head(expr_long_split)) lets us know if we’re headed in the right direction.
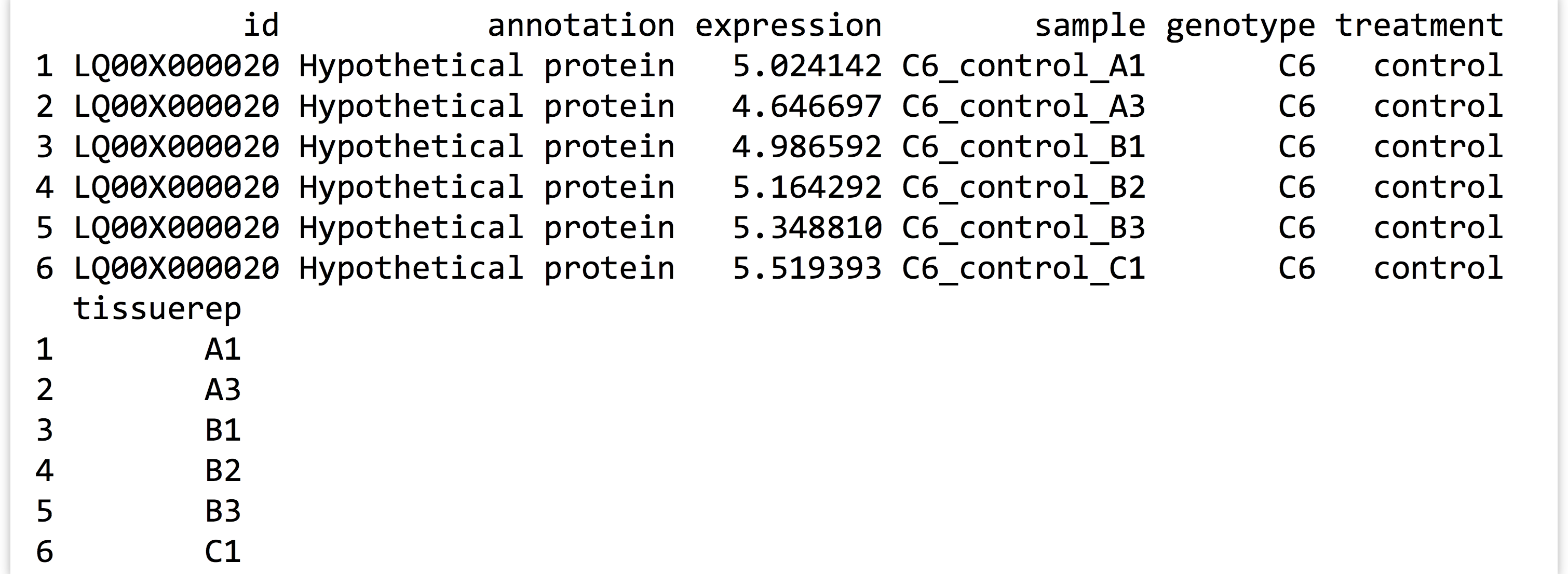
At this point, the number of columns in the data frame has grown large, so print() has elected to wrap the final column around in the printed output.
Detecting and %in%
We still don’t have separate columns for tissue and replicate, but we do have this information encoded together in a tissuerep column. Because these values are encoded without a pattern to obviously split on, str_split_fixed() may not be the most straightforward solution.
Although any solution assuming a priori knowledge of large data set contents is dangerous (as extraneous values have ways of creeping into data sets), a quick inspection of the data reveals that the tissue types are encoded as either A, B, or C, with apparently no other possibilities. Similarly, the replicate numbers are 1, 2, and 3.
A handy function in the stringr package detects the presence of a pattern in every entry of a character vector, returning a logical vector. For the column tissuerep containing "A1", "A3", "B1", "B2", "B3", "C1", ..., for example, str_detect(expr_long_split$tissuerep, "A") would return the logical vector TRUE, TRUE, FALSE, FALSE, FALSE, .... Thus we can start by creating a new tissue column, initially filled with NA values.

Then we’ll use selective replacement to fill this column with the value "A" where the tissuerep column has an "A" as identified by str_detect(). Similarly for "B" and "C".

In chapter 34, “Reshaping and Joining Data Frames,” we’ll also consider more advanced methods for this sort of pattern-based column splitting. As well, although we’re working with columns of data frames, it’s important to remember that they are still vectors (existing as columns), and that the functions we are demonstrating primarily operate on and return vectors.
If our assumption, that "A", "B", and "C" were the only possible tissue types, was correct, there should be no NA values left in the tissue column. We should verify this assumption by attempting to print all rows where the tissue column is NA (using the is.na() function, which returns a logical vector).

In this case, a data frame with zero rows is printed. There is a possibility that tissue types like "AA" have been recoded as simple "A" values using this technique—to avoid this outcome, we could use a more restrictive regular expression in the str_detect(), such as "^A\d$", which will only match elements that start with a single "A" followed by a single digit. See chapter 11, “Patterns (Regular Expressions),” and chapter 21, “Bioinformatics Knick-knacks and Regular Expressions,” for more information on regular-expression patterns.
A similar set of commands can be used to fill a new replicate column.

Again we search for leftover NA values, and find that this time there are some rows where the rep column is reported as NA, apparently because a few entries in the table have a replicate number of 0.

There are a few ways we could handle this. We could determine what these five samples’ replicate numbers should be; perhaps they were miscoded somehow. Second, we could add "0" as a separate replicate possibility (so a few groups were represented by four replicates, rather than three). Alternatively, we could remove these mystery entries.
Finally, we could remove all measurements for these gene IDs, including the other replicates. For this data set, we’ll opt for the latter, as the existence of these “mystery” measurements throws into doubt the accuracy of the other measurements, at least for this set of five IDs.
To do this, we’ll first extract a vector of the “bad” gene IDs, using logical selection on the id column based on is.na() on the rep column.

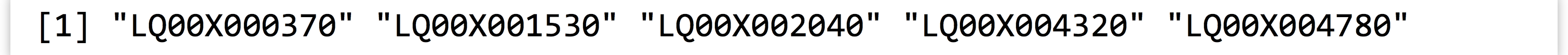
Now, for each element of the id column, which ones are equal to one of the elements in the bad_ids vector? Fortunately, R provides a %in% operator for this many-versus-many sort of comparison. Given two vectors, %in% returns a logical vector indicating which elements of the left vector match one of the elements in the right. For example, c(3, 2, 5, 1) %in% c(1, 2) returns the logical vector FALSE, TRUE, FALSE, TRUE. This operation requires comparing each of the elements in the left vector against each of the elements of the right vector, so the number of comparisons is roughly the length of the first times the length of the second. If both are very large, such an operation could take quite some time to finish.
Nevertheless, we can use the %in% operator along with logical selection to remove all rows containing a “bad” gene ID.

At this point, we could again check for NA values in the rep column to ensure the data have been cleaned up appropriately. If we wanted, we could also check length(bad_rows[bad_rows]) to see how many bad rows were identified and removed. (Do you see why?)
Pasting
While above we discussed splitting contents of character vectors into multiple vectors, occasionally we want to do the opposite: join the contents of character vectors together into a single character vector, element by element. The str_c() function from the stringr library accomplishes this task.

The str_c() function is also useful for printing nicely formatted sentences for debugging.
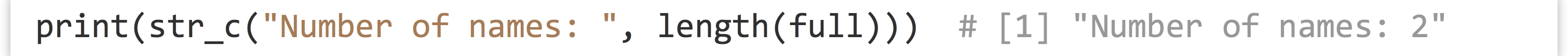
The Base-R function equivalent to str_c() is paste(), but while the default separator for str_c() is an empty string, "", the default separator for paste() is a single space, " ". The equivalent Base-R function for str_detect() is grepl(), and the closest equivalent to str_split_fixed() in Base-R is strsplit(). As mentioned previously, however, using these and other stringr functions for this type of character-vector manipulation is recommended.
Factors
By now, factors have been mentioned a few times in passing, mostly in the context of using stringsAsFactors = FALSE, to prevent character vectors from being converted into factor types when data frames are created. Factors are a type of data relatively unique to R, and provide an alternative for storing categorical data compared with simple character vectors.
A good method for understanding factors might be to understand one of the historical reasons for their development, even if the reason is no longer relevant today. How much space would the treatment column of the experimental data frame above require to store in memory, if the storage was done naively? Usually, a single character like "c" can be stored in a single byte (8 bits, depending on the encoding), so an entry like "chemical" would require 8 bytes, and "control" would require 7. Given that there are ~360,000 entries in the full table, the total space required would be ~0.36 megabytes. Obviously, the amount of space would be greater for a larger table, and decades ago even a few megabytes of data could represent a challenge.
But that’s for a naive encoding of the data. An alternative could be to encode "chemical" and "control" as simple integers 1 and 2 (4 bytes can encode integers from -2.1 to 2.1 billion), as well as a separate lookup table mapping the integer 1 to "chemical" and 2 to "control". This would be a space savings of about two times, or more if the terms were longer. This type of storage and mapping mechanism is exactly what factors provide.[1]
We can convert a character vector (or factor) into a factor using the factor() function, and as usual the head() function can be used to extract the first few elements.

When printed, factors display their levels as well as the individual data elements encoded to levels. Notice that the quote marks usually associated with character vectors are not shown.

It is illustrating to attempt to use the str() and class() and attr() functions to dig into how factors are stored. Are they lists, like the results of the t.test() function, or something else? Unfortunately, they are relatively immune to the str() function; str(treatment_factor) reports:

This result illustrates that the data appear to be coded as integers. If we were to run print(class(treatment_factor)), we would discover its class is "factor".
As it turns out, the class of a data type is stored as an attribute.

Above, we learned that we could remove an attribute by setting it to NULL. Let’s set the "class" attribute to NULL, and then run str() on it.


Aha! This operation reveals a factor’s true nature: an integer vector, with an attribute of "levels" storing a character vector of labels, and an attribute for "class" that specifies the class of the vector as a factor. The data itself are stored as either 1 or 2, but the levels attribute has "chemical" as its first element (and hence an integer of 1 encodes "chemical") and "control" as its second (so 2 encodes "control").
This special "class" attribute controls how functions like str() and print() operate on an object, and if we want to change it, this is better done by using the class() accessor function rather than the attr() function as above. Let’s change the class back to factor.

Renaming Factor Levels
Because levels are stored as an attribute of the data, we can easily change the names of the levels by modifying the attribute. We can do this with the attr() function, but as usual, a specific accessor function called levels() is preferred.

Why is the levels() function preferred over using attr()? Because when using attr(), there would be nothing to stop us from doing something irresponsible, like setting the levels to identical values, as in c("Water", "Water"). The levels() function will check for this and other absurdities.
What the levels() function can’t check for, however, is the semantic meaning of the levels themselves. It would not be a good idea to mix up the names, so that "Chemical" would actually be referring to plants treated with water, and vice versa:

The reason this is a bad idea is that using levels() only modifies the "levels" attribute but does nothing to the underlying integer data, breaking the mapping.
Reordering Factor Levels
Although we motivated factors on the basis of memory savings, in modern versions of R, even character vectors are stored internally using a sophisticated strategy, and modern computers generally have larger stores of RAM besides. Still, there is another motivation for factors: the fact that the levels may have a meaningful order. Some statistical tests might like to compare certain subsets of a data frame as defined by a factor; for example, numeric values associated with factor levels "low" might be compared to those labeled "medium", and those in turn should be compared to values labeled "high". But, given these labels, it makes no sense to compare the "low" readings directly to the "high" readings. Factors provide a way to specify that the data are categorical, but also that "low" < "medium" < "high".
Thus we might like to specify or change the order of the levels within a factor, to say, for example, that the "Water" treatment is somehow less than the "Chemical" treatment. But we can’t do this by just renaming the levels.
The most straightforward way to specify the order of a character vector or factor is to convert it to a factor with factor() (even if it already is a factor) and specify the order of the levels with the optional levels = parameter. Usually, if a specific order is being supplied, we’ll want to specify ordered = TRUE as well. The levels specified by the levels = parameter must match the existing entries. To simultaneously rename the levels, the labels = parameter can be used as well.

Now, "Water" is used in place of "control", and the factor knows that "Water" < "Chemical". If we wished to have "Chemical" < "Water", we would have needed to use levels = c("chemical", "control") and labels = c("Chemical", "Water") in the call to factor().

Disregarding the labels = argument (used only when we want to rename levels while reordering), because the levels = argument takes a character vector of the unique entries in the input vector, these could be precomputed to hold the levels in a given order. Perhaps we’d like to order the tissue types in reverse alphabetical order, for example:


Rather than assigning to a separate tissues_factor variable, we could replace the data frame column with the ordered vector by assigning to expr_long_split$tissue.
We often wish to order the levels of a factor according to some other data. In our example, we might want the “first” tissue type to be the one with the smallest mean expression, and the last to be the one with the highest mean expression. A specialized function, reorder(), makes this sort of ordering quick and relatively painless. It takes three important parameters (among other optional ones):
- The factor or character vector to convert to a factor with reordered levels.
- A (generally numeric) vector of the same length to use as reordering data.
- A function to use in determining what to do with argument 2.
Here’s a quick canonical example. Suppose we have two vectors (or columns in a data frame), one of sampled fish species (“bass,” “salmon,” or “trout”) and another of corresponding weights. Notice that the salmon are generally heavy, the trout are light, and the bass are in between.

If we were to convert the species vector into a factor with factor(species), we would get the default alphabetical ordering: bass, salmon, trout. If we’d prefer to organize the levels according to the mean of the group weights, we can use reorder():

With this assignment, species_factor will be an ordered factor with trout < bass < salmon. This small line of code does quite a lot, actually. It runs the mean() function on each group of weights defined by the different species labels, sorts the results by those means, and uses the corresponding group ordering to set the factor levels. What is even more impressive is that we could have just as easily used median instead of mean, or any other function that operates on a numeric vector to produce a numeric summary. This idea of specifying functions as parameters in other functions is one of the powerful “functional” approaches taken by R, and we’ll be seeing more of it.
Final Notes about Factors
In many ways, factors work much like character vectors and vice versa; %in% and == can be used to compare elements of factors just as they can with character vectors (e.g., tissues_factor == "A" returns the expected logical vector).
Factors enforce that all elements are treated as one of the levels named in the levels attribute, or NA otherwise. A factor encoding 1 and 2 as male and female, for example, will treat any other underlying integer as NA. To get a factor to accept novel levels, the levels attribute must first be modified with the levels() function.
Finally, because factors work much like character vectors, but don’t print their quotes, it can be difficult to tell them apart from other types when printed. This goes for simple character vectors when they are part of data frames. Consider the following printout of a data frame:

Because quotation marks are left off when printing data frames, it’s impossible to tell from this simple output that the id column is a character vector, the tissue column is a factor, the count column is an integer vector, and the group column is a factor.[2] Using class() on individual columns of a data frame can be useful for determining what types they actually are.
Exercises
- In the annotation file
PZ.annot.txt, each sequence ID (column 1) may be associated with multiple gene ontology (GO) “numbers” (column 2) and a number of different “terms” (column 3). Many IDs are associated with multiple GO numbers, and there is nothing to stop a particular number or term from being associated with multiple IDs. While most of the sequence IDs have an underscore suffix, not all do. Start by reading in this file (columns are tab separated) and then extracting a
While most of the sequence IDs have an underscore suffix, not all do. Start by reading in this file (columns are tab separated) and then extracting a suffix_onlydata frame containing just those rows where the sequence ID contains an underscore. Similarly, extract ano_suffixdata frame for rows where sequence IDs do not contain an underscore.Next, add to the
suffix_onlydata frame columns forbase_idandsuffix, where base IDs are the parts before the underscore and suffices are the parts after the underscore (e.g.,base_idis"PZ7180000023260"andsuffixis"APN"for the ID"PZ7180000023260_APN").Finally, produce versions of these two data frames where the
GO:prefix has been removed from all entries of the second column. - The line
s <- sample(c("0", "1", "2", "3", "4"), size = 100, replace = TRUE)generates a character vector of 100 random"0"s,"1"s,"2"s,"3"s, and"4"s.Suppose that"0"means “Strongly Disagree,”"1"means “Disagree,”"2"means “Neutral,”"3"means “Agree,” and"4"means “Strongly Agree.” Convertsinto an ordered factor with levelsStrongly Disagree < Disagree < Neutral < Agree < Strongly Agree. - Like vectors, data frames (both rows and columns) can be selected by index number (numeric vector), logical vector, or name (character vector). Suppose that
grade_currentis a character vector generated bygrade_current <- sample(c("A", "B", "C", "D", "E"), size = 100, replace = TRUE), andgpais a numeric vector, as ingpa <- runif(100, min = 0.0, max = 4.0). Further, we add these as columns to a data frame,grades <- data.frame(current_grade, gpa, stringsAsFactors = FALSE).We are interested in pulling out all rows that have
"A","B", or"C"in thecurrent_gradecolumn. Describe, in detail, what each of the three potential solutions does: How does R interpret each one (i.e., what will R try to do for each), and what would the result be? Which one(s) is (are) correct? Which will report errors? Are the following three lines any different from the above three in what R tries to do?
How does R interpret each one (i.e., what will R try to do for each), and what would the result be? Which one(s) is (are) correct? Which will report errors? Are the following three lines any different from the above three in what R tries to do?
- Although character vectors are also efficiently stored in modern-day versions of R, factors still have unique uses. ↵
- Factors created from integer vectors are a special kind of headache. Consider a line like
h <- factor(c(4, 1, 5, 6, 4)); because factors are treated like character types, this would be converted so it is based onc("4", "1", "5", "6", "4"), where the underlying mapping and storage have an almost arbitrary relationship to the elements. Tryprint(as.numeric(h))to see the trouble one can get into when mixing up these types, as well asclass(h) <- NULLfollowed bystr(h)to see the underlying mapping and why this occurs. ↵

