Unit 5: Exploring the Nature of Astronomical Phenomena in the Context of the Sun/Earth/Moon System
XI. Pondering Additional Issues
This section explores several additional issues: how things move and interact, what keeps the Moon and the Earth in their orbits, why the oceans have tides, and what happens when objects fall here on Earth and on the Moon?
A. Reviewing understandings about the Sun, Earth, Moon, and Stars
It may be helpful to step back and review before heading into new territory. So far this course has developed the following understandings about light and shadows as well as about the Sun, Earth, Moon, and stars:
What causes shadows? Some shadows occur when an object blocks light and casts a shadow behind it on something else. Other shadows occur when an object blocks light from shining on its own back-side. If you stand facing the Sun on a sunny day, for example, your shadow forms on the ground or a wall behind you; a shadow also forms on your back because your body blocks sunlight from shining there.
Why does it get dark at night? The Sun seems to rise in the morning, move high across the sky during the day, and set in the evening. It gets dark when the Sun appears to sink below the horizon in the western sky and stays dark until the Sun appears to rise above the horizon again in the eastern sky. According to this conceptual model, it gets dark at night because the source of light, the Sun, has moved below the horizon during its apparent daily journey revolving around the fixed Earth. This Fixed Earth, Revolving Sun model is easy to envision and believe because that is what one sees: the Sun, as well as the Moon and many stars, seeming to move daily around a flat motionless Earth.
An alternative conceptual model, however, is that the Sun, Moon, and stars only appear to be moving daily around the Earth; instead it is the Earth that actually is moving, a spherical Earth rotating daily on its axis. According to this conceptual model, it is day on the front side of the spinning Earth, the side that is facing toward a fixed Sun; it is night on the back side of the spinning Earth, the side that is facing away from a fixed Sun. It gets dark at night because the back side of the rotating Earth is in the Earth’s own shadow. According to this Rotating Earth, Fixed Sun model, the body of the Earth itself is blocking the Sun’s light from shining on the side of the Earth that is facing away from the Sun.
The Rotating Earth, Fixed Sun model is not as easy to envision as the Fixed Earth, Revolving Sun model. Acting out these two conceptual models for explaining day and night, however, can clarify how these models are alike and different. Also seeing a physical model can help, such as a spinning globe near a lamp in a dark room, particularly if a tiny flag or stick figure stuck to the globe represents a familiar location on the rotating Earth. Understanding and accepting the Rotating Earth, Fixed Sun model requires, however, more detailed observations and intricate reasoning than simply seeing the Sun, Moon, and stars seem to move across the sky on daily journeys revolving around the Earth.
Why does the Moon seem to have different shapes at different times? During about a month, the Moon’s shape seems to keep changing, with the lit portion seeming to grow more and more lit until full and then shrinking back to not being visible at all (see Fig. 5.22). Many people believe that these changing phases of the Moon are caused by the shadow of the Earth falling on the Moon. Such a conceptual model matches experiences in which one often sees an object casting a shadow behind it onto something else.
An alternative conceptual model is that the lit shape of the Moon appears to change during about a month, as seen from Earth, because the Moon is revolving around the Earth. The side of the Moon facing toward the Sun is brightly lit by the Sun; the side of the Moon facing away from the Sun is dark, in the Moon’s own shadow. According to this Revolving Moon model, the Moon’s changing phases as seen from Earth occur because different portions of the lit side are visible from Earth as the Moon revolves around the Earth about once a month (See Figs. 5.42 and 5.43).
Envisioning the Revolving Moon model is easier if one plays with a ball on a sunny day or in a dark room lit by a single lamp. The ball represents the Moon, the Sun or lamp represents the Sun, and one’s eyes in one’s head represent one’s eyes here on the Earth. By holding up the ball and moving it around one’s head, one can replicate on the ball the same pattern of changing phases one can see in the sky on the Moon: “new ball” “waxing crescent ball” “first quarter ball” “waxing gibbous ball” “full ball” “waning gibbous ball” “third quarter ball” and “waning crescent ball” positions back to “new ball.” Replicating with a ball here on Earth the same sequence of phases of the Moon that one can see in the sky suggests that these have the same cause: the Moon is revolving around the Earth just as the ball is revolving around one’s head.
On-going observations of the Moon can reveal a paradox: Why does the Moon seem to move east to west over several hours but west to east over several days? (See Figs. 5.31 and 5.32.) One can infer that the Moon appears to move from west to east over several days because the Moon actually is moving that way while revolving around the Earth about once a month. One also can infer that the Moon only appears to move daily across the sky from east to west because it is the Earth that actually is moving, spinning by the Moon while rotating daily on its axis. Thus the resolution of this paradox uses and confirms one of the two models developed earlier for explaining day and night, the Rotating Earth, Fixed Sun model.
Why are some constellations of stars only visible during certain seasons? Both ancient and current conceptual models assume that the daytime sky is too bright for stars located in the same direction as the Sun to be visible. According to the conceptual model used by many ancient astronomers (Fixed Earth, Revolving Sun), stars revolve around the Earth daily on a large crystalline sphere; the Sun revolves around the Earth daily on a smaller sphere and also moves yearly along a path with respect to the background sphere of the stars. The Sun’s position on this path, called the zodiac (See Fig. 5.67), determines which stars would be visible, those not in the same direction as the Sun.
An alternative conceptual model is that some stars are only visible during certain seasons because a rotating Earth revolves around the Sun. The direction on Earth of facing away from the Sun determines which stars one sees at night. These change as the Earth travels in its orbit so that different constellations of stars are visible at different times. This is based upon the currently accepted conceptual model of a spherical Earth that rotates daily on its axis while revolving yearly around the Sun.
B. Understanding motion
Scientific progress occurs through the processes just described of making observations, developing possible explanatory models, and thinking about which models together make the most sense. Typically new questions emerge. If the Moon and the Earth are both moving, for example, how does that happen?
Question 5.47 How are the Moon and the Earth moving?
- Place the ball on the floor so that the ball is not moving.
- Give the ball a push. How does the ball roll along the floor?
- How can you change the ball’s direction of motion while it is moving?
- How can you make the ball move in a circle?
An English scientist, Sir Isaac Newton, studied motion in the late 1600’s and early 1700’s. He summarized his findings in a major work, Philosophiae Naturalis Principia Mathematica published in Latin in 1687 and in English, translated by Andrew Motte, as Mathematical Principles of Natural Philosophy in 1729.

The Principia included three books. Book 1 focused upon the motion of bodies, Book 2 upon the motion of bodies in resisting mediums, and Book 3 on the system of the world. The contents of these volumes have deeply influenced the development of science and society for more than three centuries.
Near the beginning of Book 1, Newton stated Axioms or Laws of Motion, including Law I:
Law I
Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.
(Newton, trans. by Motte, 1729, Book I, Axioms or Laws of Motion)
https://archive.org/details/100878576/page/82
According to Newton’s First Law of Motion, an object at rest stays at rest or if already in motion, keeps moving at the same speed in a straight line, unless acted on by a force.
Newton’s Second Law of Motion addressed what happens if a force acts on a moving object: the object changes its speed and/or direction of motion. If the Moon and the Earth are moving but not in straight lines, what forces might be acting on them to cause their paths to curve?
C. Exploring forces
If one object affects another object in some way, there must be some kind of an interaction happening between them. In physics, the word force refers to an interaction between objects, such as pushing or pulling on one another.
Exploring how things push or pull on one another here on Earth can provide some experiences on which to base thinking about forces that might be causing the Moon to revolve around the Earth and the Earth to revolve around the Sun.
Question 5.48 What keeps the Moon and the Earth revolving in their orbits?
- Discuss with your group members some experiences that you have had with things that are pushing or pulling on one another while:
- touching
- not touching
- moving
- not moving
- Play with the two magnets. How do they interact?
- Play with the ball on a string. How do the ball and the string interact if you swing the ball on the string around your head?
(Careful! Be sure you have enough space around you to swing the ball without hitting anyone; also take care to swing without hitting yourself.)
- How would you describe the interaction between the Moon and the Earth as similar and/or different from the interactions:
- between the two magnets?
- between the ball and string when you are swinging the ball around your head?
If touching, two magnets may stick together and be hard to pull apart. If brought near but not touching and then released, two magnets may attract one another and move closer together. Or they may repel one another and move farther apart. Such observations indicate that two magnets can interact with one another even though they are not touching.
The interactions between the Moon and the Earth as well as between the Earth and the Sun are similar to the interaction between the magnets in that these bodies also are not touching. These are examples of forces that act at a distance because the interactions occur without the objects being close enough to touch one another.
The forces that two magnets exert on one another can be attractive or repulsive in effect.
The interactions between the Moon and the Earth as well as between the Earth and the Sun are different, however, in that these appear to be only attractive effects; these bodies do not appear to be pushing one another apart.
A ball being swung around one’s head is pulled inward by the string, which keeps the ball moving in the curved path of its orbit. The orbital motion of the ball seems to be similar to the orbital motion of the Moon. This suggests that there is a similar inward pull on the Moon by the Earth that keeps the Moon moving in the curved path of its orbit.
This is called the gravitational force by the Earth on the Moon. In the Principia, Newton expressed this as a Proposition and Theorem:
PROPOSITION IV. THEOREM IV.
That the moon gravitates towards the earth, and by the force of gravity is continually drawn off from a rectilinear motion, and retained in its orbit.
(Newton, trans. by Motte, 1729, Book III, Propositions)
https://archive.org/details/100878576/page/390
Similarly there is an inward pull by the Sun on the Earth that is keeping the Earth in its orbit. This is called the gravitational force by the Sun on the Earth. When one object is revolving around another, the gravitational force by the larger object on the smaller object keeps the smaller object in its orbit.
These gravitational forces are similar to the string pulling inward on the swinging ball. They differ from the force by the string on the ball, however, in that these bodies are not touching one another; the gravitational forces are acting at a distance without touching.
This conceptual model of a gravitational force pulling the Moon inward toward the Earth as the Moon revolves around the Earth raises a new issue: is this interaction between the Moon and the Earth mutual?
Question 5.49 If the Earth pulls on the Moon, does the Moon pull on the Earth?
- Explore what happens here on Earth when two spring scales are pulled apart.
If you pull on a spring scale, it will measure the force with which you are pulling, usually either in pounds or in Newtons. A Newton is a unit of force in the metric system, named after Sir Isaac Newton. The front of the device hides the spring. Spring scales work by stretching a spring uniformly when the scale is pulled so that the indicator moves a distance proportional to the force applied. As shown in Fig. 5.90 spring scales may be circular or rectangular in shape.
- Play with the spring scales until you understand how they work.
- Have two members of the group hook the two spring scales together and then pull the spring scales apart horizontally. What do you notice?
- Have every member of the group try this. Are your findings consistent?
- What happens when the two people both pull on the spring scales?
- What happens when one person just holds the spring scale that is hooked on to the other person’s spring scale while the other person pulls?
- Sketch a picture of what is happening when two people both pull horizontally on spring scales that are hooked together.
- Also sketch what happens when only one person pulls a scale and the other person just holds on to the other scale.
- What do you think would happen if instead of a person just holding on to a scale, the scale is hooked to a wall while the other person pulls on the other scale?
- Can an inanimate object like a wall exert a force?
- Summarize your findings.
Among the laws of motion that Newton stated was Law III:
Law III
To every Action there is always opposed an equal Reaction: or the mutual actions of two bodies upon each other are always equal and directed to contrary parts.
He provided an example:
Whatever draws or presses another is as much drawn or pressed by that other. If you press a stone with your finger, the finger is also pressed by the stone…
(Newton, trans. by Motte, 1729, Book I, Axioms or Laws of Motion, p. 83)
https://archive.org/details/100878576/page/82
Newton realized that forces come in pairs; if you press on a stone, the stone presses back with an equal force in the opposite direction. See (http://hyperphysics.phy-astr.gsu.edu/hbase/Newt.html#ntcon) for additional discussion of Newton’s three laws of motion.
As shown in Fig. 5.91, two spring scales pulled apart indicate that the force by the left scale on the right scale is equal to the force by the right scale on the left scale but in the opposite direction.

This has some surprising consequences.
- Push straight down on a table. With what force is the table pushing back up at you?
- How can you justify your response?
D. Developing and using mathematical representations of gravitational forces
In addition to formulating and articulating ways to use the three laws of motion, Sir Isaac Newton also presented a detailed account of interactions between bodies due to gravitational forces.
Question 5.50 What quantities determine the magnitude of gravitational forces?
In Book III of the Principia, Newton proposed that the Sun’s gravitational effect on keeping the Earth and other planets in their orbits depends upon how far away they are:
PROPOSITION II. THEOREM II.
That the forces by which the primary planets are continually drawn off from rectilinear motions, and retained in their proper orbits, tend to the sun; and are reciprocally as the squares of the distance of the places of those planets from the sun’s center.
(Newton, trans. by Motte, 1729, Book III, Propositions, p. 390)
https://archive.org/details/100878576/page/390
Newton specified that this was a reciprocal relationship; the closer a planet to the Sun, the bigger the gravitational force by the Sun on the planet, keeping that planet in its orbit, and that mathematically this was a function of the reciprocal of the distance multiplied by itself (the distance squared).
In addition Newton proposed that a gravitational effect occurred with all bodies in the universe and depended upon their masses:
PROPOSITION VII. THEOREM VII.
That there is a power of gravity tending to all bodies, proportional to the several quantities of matter which they contain.
(Newton, trans. by Motte, 1729, Book III, Propositions, p. 397)
https://archive.org/details/100878576/page/396
Stated algebraically, this is known as Newton’s Law of Universal Gravitation, where the gravitational force (F) exerted by one mass (M) on another mass (m) depends upon the size of the masses (M, m) and the inverse square of the distance (r) between them:
[latex]F = \frac{GMm}{r^2}[/latex]
where G is the Gravitational Constant, G = 6.67430 x 10-11 [latex]\frac{Newton- \, meters^2}{kilograms^2}[/latex]
This means that the gravitational force by Body A on Body B is equal in magnitude and opposite in direction to the gravitational force by Body B on Body A.
This proposition has some startling implications. Not only does the gravitational force by the mass of the Earth pull on the Moon, it pulls on you as well! The gravitational force by the Earth on you is what is holding you on the ground rather than floating in space. You are pushing back on the Earth (the ground) with an equal and opposite force! Not only that, but as you work together in class, you and your group members also are pulling on each other with equal and opposite gravitational forces (but not noticeably).
E. Explaining the ocean’s tides
Newton’s Law of Universal Gravitation suggests that the Moon is pulling on the Earth with a force of the same magnitude as the Earth is pulling on the Moon, although in the opposite direction. What evidence is there that this is the case?
Question 5.51 What effect does the gravitational force by the Moon have on the Earth?
People who walk on ocean beaches often notice how far waves are flowing onto shore. People who work on boats tied up to docks often notice how high the boats are floating compared to the height of the dock. This sometimes varies by as much as 45 feet. (See: https://tidesandcurrents.noaa.gov/education.html) Many variables affect tides such as a location’s latitude, the shape of its shoreline, shape of a bay and/or estuaries, nearby ocean currents, local winds and weather.
By observing and recording daily tide levels, however, one can identify patterns and make predictions for future dates. Detailed predictions depend upon repeated measurements at a tide-monitoring station and upon complex computer modeling of such data (http://oceanmotion.org/html/background/tides-observing.htm)
As shown in Fig. 5.92, for example, the National Oceanic and Atmospheric Administration (NOAA) provides monthly predictions of the variation in water level at the Yaquina Bay United States Coast Guard station in Newport, Oregon.
- Interpret this graph: What does the horizontal axis represent? What does the vertical axis represent? What does the line represent? What does the shape of the line represent?
- Discuss with your group members how high and low tides are predicted to vary over this month at this tidal monitoring station:
- When are high tides higher than usual and low tides lower than usual so that there is a big difference between high and low tides at this location?
- When are the high tides not so high and the low tides not so low so that there is a smaller difference between high and low tides at this location?
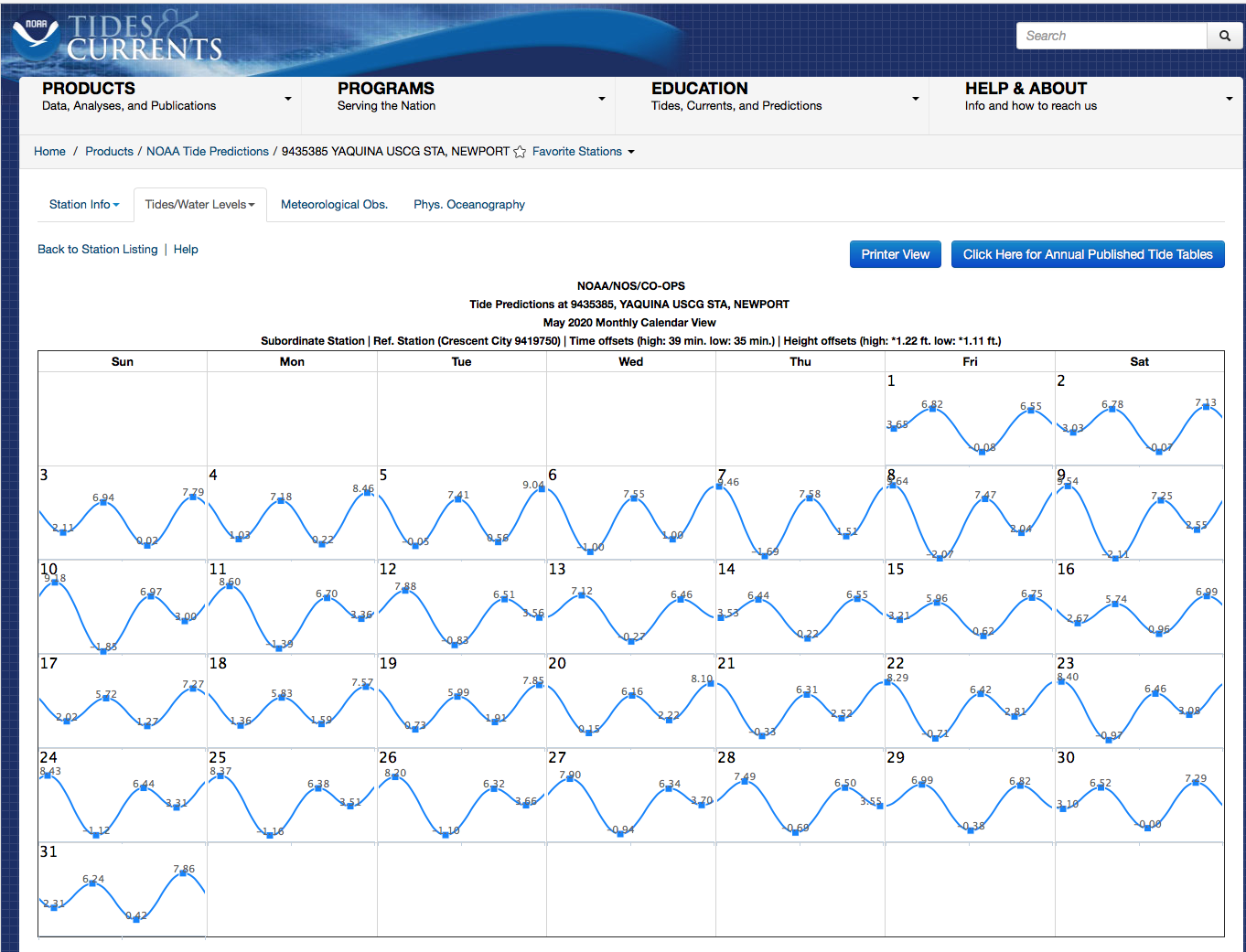
People who live near the ocean may notice a pattern between tidal phenomena and the phases of the Moon.
- Of what connections are you already aware between tidal and Moon phenomena?
- How might you explore this relationship using additional Internet resources?
- Do an Internet search, for example, for “moon phases calendar.” Websites such as https://www.almanac.com/astronomy/moon/calendar or https://www.calendar-365.com/moon/moon-calendar.html can provide a monthly calendar of the changing phases of the Moon.
- Enter May 2020 to see the changing phases of the Moon during the same month and year of the tide chart shown in Fig. 5.92. Enter the location of Newport, Oregon, if the moon calendar website includes an option for entering a location.
- Discuss with your group members any patterns you see in the tides predicted in Fig. 5.92 and the predicted phases of the Moon for this time period shown in the moon calendar you are viewing online.
- How are these phases of the Moon related to times of predicted highest high tides and lowest low tides evident in Fig. 5.92?
- How are the phases of the Moon related to times of predicted somewhat high and low tides?
- With your group members, develop a central idea about the relation between the phases of the Moon and tides on the Earth, based upon the predictions of the tidal patterns shown in Fig. 5.92 and of the phases of the Moon shown in the moon calendar you are viewing on the website.
Viewing the entire month of predicted high and low tides, as well as the entire month of predicted phases of the Moon may seem overwhelming. A way to simplify the task would be to look at what is happening during only the primary phases of the Moon (first quarter, full, third quarter, and new).
- Fig. 5.93 shows predictions for the primary phases of the Moon at, Newport, Oregon for the month of May, 2020.

(If you want to compare tide predictions with moon phases for a different place or month, be sure to obtain the dates for phases of the moon for that location. The Sun, Earth, and Moon are lined up at the moment of full moon but the name of this moment depends upon a location’s longitude. The predicted time of full moon, for example, in May 2020 is at 3:45 a.m. on May 7 in Newport, Oregon, but at 11:45 a.m., on May 7 universal time in Greenwich, England, and at 8:45 p.m. on May 7 in Melbourne, Australia. For dates and times of phases of the Moon at different locations see https://www.timeanddate.com/moon/phases/ . Enter your location and current date, record the predicted date for the closest major phase of the moon (new, 1st quarter, full, third quarter). For tidal predictions elsewhere, see https://tidesandcurrents.noaa.gov/stations.html?type=Water+Levels.)
Interpreted visually, the calendar for May 2020 at the Yaquina US Coast Guard Station in Newport, Oregon, predicts the highest and lowest tides near the middle to the end of the week of May 3, and somewhat varying high and low tides near the middle to the end of the week of May 10. A less visually salient pattern is evident during the weeks of May 17 and May 24. Near the middle to the end of the week of May 17, the regular pattern of very high and very low tides seems similar to near the middle to the end of the week of May 7 although less extreme. Near the middle to the end of the week of May 24, somewhat varying high and low tides seem similar to near the middle to the end of the week of May 10.
First quarter, full, third quarter, new, and first quarter phases of the Moon are predicted to occur during Thursdays or Fridays during late April and May 2020 (see, for example, https://www.timeanddate.com/moon/phases/usa/newport-or?year=2020. Using the information provided in the tide calendar in Fig. 5.92, the predicted high and low tides can be compared numerically during these phases as shown in Tables V.14 and V.15.
| Table V.14 Predicted high and low tides during the predicted dates of full, 3rd quarter, new, and 1st quarter phases of the Moon during May 2020 at the Yaquina Coast Guard Station, in Newport, Oregon | ||||
|---|---|---|---|---|
| Phase and Date | 1st High tide | 1st Low tide | 2nd High tide | 2nd Low tide
|
| Full Moon on May 7
|
9.46 ft | -1.69 ft | 7.58 ft | 1.51 ft |
| 3rd Quarter Moon on May 14 | 6.44 ft | 0.22 ft | 6.55 ft | 3.21 ft (very early on May 15) |
| New Moon on May 22
|
8.29 ft | -0.71 ft | 6.42 ft | 2.81 ft |
| 1st Quarter Moon on May 29
|
6.99 ft | -0.38 ft | 6.82 ft | 3.10 ft (very early on May 30) |
A low tide with a negative height, -1.69 feet, is predicted at 6:56 a.m. for May 7. This is a very low tide, lower than the average low tide for a particular tide-monitoring station, which is typically set as the zero point for that station. A minus tide means that tide pools usually under water would be exposed and interesting to explore at low tide early on this date.
To simplify looking for patterns, it sometimes helps to combine data such as calculating average high tides for a given date, average low tides for that date, and then the difference between the average high and low tides as shown in Table V.15.
- What patterns are evident when comparing particular phases of the Moon with:
- average predicted high tides
- average predicted low tides
- bigger differences between the average predicted high and low tides
- smaller differences between the average predicted high and low tides
at the Yaquina Coast Guard Station at Newport, Oregon, during the full, third quarter, new, and first quarter phases of the Moon during May 2020?
| Table V.15 Average predicted high and low tides during the predicted full, 3rd quarter, new, and 1st quarter phases of the Moon during May 2020 at the Yaquina Coast Guard Station, in Newport, Oregon | |||
|---|---|---|---|
| Moon Phase and Date | Average predicted high tide in feet | Average predicted low tide in feet | Difference between average predicted high and low tides |
| Full Moon on May 7 | 8.52 | -0.09 | 8.61
|
| 3rd Quarter Moon on May 14 | 6.50 | 1.71 | 4.70
|
| New Moon on May 22
|
7.36 | 1.05 | 6.31 |
| 1st Quarter Moon on May 29
|
6.91 | 1.36 | 5.55
|
The average highest high tides and lowest low tides are predicted to occur during the full and new moon phases during May 2020 in Newport. The biggest differences between the average high and low tides are predicted to occur during these full and new moon phases.
Smaller average high tides and bigger average low tides are predicted to occur during third and first quarter moon phases during May 2020 in Newport. The smallest differences between the average high and low tides are predicted to occur during these third and first quarter phases.
These patterns connecting variations in the ocean’s tides with the phases of the Moon support the claim that a gravitational force by the Moon on the Earth exists. A gravitational force by the Sun also acts on the Earth’s oceans and affects the tides, depending upon how the Sun, Earth, and Moon are arranged in space.
Question 5.52 How do gravitational forces by the Moon and by the Sun on the Earth’s oceans affect the tides?
- Draw the view from space, as in Fig. 5.38, for the arrangements of the Sun, Earth, and Moon for new, first quarter, full, and third quarter phases.
- Discuss with your group members which of these arrangements would produce the most effect from gravitational forces by the Sun and by the Moon on the Earth’s oceans. Which arrangements would affect the Earth’s oceans the least?
As shown in Fig. 5.94, during the new and full moon phases, the Sun, Earth, and Moon are arranged in a straight line, with the moon between the Sun and Earth, or beyond the Earth:

During new and full moon phases, the effects of the gravitational forces by both the Sun and the Moon contribute to creating bulges of water along this straight line. The gravitational force by the Sun and the gravitational force by the Moon on the Earth’s oceans are directly in line during new and full Moon and therefore cause the highest high tides and lowest low tides as the Earth rotates on its axis. These are called spring tides, not because they occur only in the spring but because they can be considered as “springing forth” during new and full moons. (For more information about spring tides see https://oceanservice.noaa.gov/facts/springtide.html)
As shown in Fig. 5.95, during first and third quarter phases, the Sun, Earth, and Moon are arranged at right angles with Earth at the vertex, as would be seen from above the solar system while looking down on the northern hemisphere:

During first and third quarter phases, the effect of the gravitational force by the Sun on the Earth’s oceans causes bulges of water in one direction and the effect of the gravitational force by the Moon on the Earth’s oceans causes bulges of water at right angles so these effects together produce smaller net bulges of water as the Earth rotates on its axis. These are called neap tides, a term apparently derived from an old English word for narrow. (For more information about neap tides see: http://earthsky.org/earth/tides-and-the-pull-of-the-moon-and-sun#neap-tides).
There are bulges of water on both sides of the Earth, which in most places produce two daily high tides as the Earth rotates by a given location. Explanations of the second bulge refer to the difference in gravitational effects on opposite sides of the Earth and on the rigidity of land masses such as continents versus fluidity of water. (see http://earthsky.org/earth/tides-and-the-pull-of-the-moon-and-sun)
Additional variations in high and low tides occur due to variations in the distances between the Earth and the Moon and between the Earth and the Sun because the orbits of the Moon and of the Earth are not perfect circles but ellipses. See http://astunit.com/astunit_tutorial.php?topic=tides and http://oceanservice.noaa.gov/education/kits/tides/tides06_variations.html.
F. Exploring falling objects
One effect of the Earth’s gravitational force on objects is that they fall down if dropped.
Question 5.53 What happens when heavy and light objects are dropped from the same height at the same time?
- Respond to the following diagnostic question to document your initial knowledge about falling objects.
1. Documenting initial knowledge about falling objects
Name_____________________ Date__________
Falling Objects Diagnostic Question
Two balls are dropped from the same height at the same instant. The balls have the same diameter but different weights.
Which hits the ground first, the heavy ball or the light ball? Or do they both land at the same time? Why?
2. Role playing Galileo’s dialogue about falling objects
A Greek philosopher, Aristotle (384–322 BC), stated that heavier objects fall faster than light objects. His ideas were influential for about 2000 years. In 1638, an Italian scientist, Galileo Galilei, wrote a dialogue in which three people discussed this question. In his Dialogue Concerning Two New Sciences, Salviati, Sagredo, and Simplicio have a conversation about this topic:
Excerpt from: Galileo Galilei (1638 /1914). Dialogue concerning two new sciences. H. Crew & A. de Salvio (trans.), New York: Macmillan.
SALVIATI, SAGREDO AND SIMPLICIO are discussing motion:
SALV. …I greatly doubt that Aristotle ever tested by experiment whether it be true that two stones, one weighing ten times as much as the other, if allowed to fall, at the same instant, from a height of, say, 100 cubits, would so differ in speed that when the heavier had reached the ground, the other would not have fallen more than 10 cubits.
SIMP. His language would seem to indicate that he had tried the experiment, because he says: We see the heavier; now the word see shows that he had made the experiment.
SAGR. But I, Simplicio, who have made the test can assure you that a cannon ball weighing one or two hundred pounds, or even more, will not reach the ground by as much as a span ahead of a musket ball weighing only half a pound, provided both are dropped from a height of 200 cubits.
SALV. But, even without further experiment, it is possible to prove clearly, by means of a short and conclusive argument, that a heavier body does not move more rapidly than a lighter one provided both bodies are of the same material and in short such as those mentioned by Aristotle…
SALV. If then we take two bodies whose natural speeds are different, it is clear that on uniting the two, the more rapid one will be partly retarded by the slower, and the slower will be somewhat hastened by the swifter. Do you not agree with me in this opinion?
SIMP. You are unquestionably right.
SALV. But if this is true, and if a large stone moves with a speed of, say, eight while a smaller moves with a speed of four, then when they are united, the system will move with a speed less than eight; but the two stones when tied together make a stone larger than that which before moved with a speed of eight. Hence the heavier body moves with less speed than the lighter; an effect which is contrary to your supposition. Thus you see how, from your assumption that the heavier body moves more rapidly than the lighter one, I infer that the heavier body moves more slowly.
SIMP. I am all at sea because it appears to me that the smaller stone when added to the larger increases its weight and by adding weight I do not see how it can fail to increase its speed or, at least, not to diminish it…
SALV. …but we have already concluded that when the small stone moves more slowly it retards to some extent the speed of the larger, so that the combination of the two, which is a heavier body than the larger of the two stones, would move less rapidly, a conclusion which is contrary to your hypothesis. We infer therefore that large and small bodies move with the same speed provided they are of the same specific gravity.
SIMP. Your discussion is really admirable; yet I do not find it easy to believe that a bird-shot falls as swiftly as a cannon ball.
SALV. Why not say a grain of sand as rapidly as a grindstone? But, Simplicio, I trust you will not follow the example of many others who divert the discussion from its main intent and fasten upon some statement of mine which lacks a hairsbreadth of the truth and, under this hair, hide the fault of another which is as big as a ship’s cable. Aristotle says that “an iron ball of one hundred pounds falling from a height of one hundred cubits reaches the ground before a one-pound ball has fallen a single cubit.” I say that they arrive at the same time. You find, on making the experiment, that the larger outstrips the smaller by two finger-breadths, that is, when the larger has reached the ground, the other is short of it by two finger-breadths; now you would not hide behind these two fingers the ninety-nine cubits of Aristotle, nor would you mention my small error and at the same time pass over in silence his very large one.
Galileo’s logical argument has three parts:
Salviati: “If then we take two bodies whose natural speeds are different, it is clear that on uniting the two, the more rapid one will be partly retarded by the slower, and the slower will be somewhat hastened by the swifter.”
(If tie two bodies together, they should fall slower because light one drags the heavier back)
Salviati: …the combination of the two, which is a heavier body than the larger of the two stones, would move less rapidly, a conclusion which is contrary to your hypothesis (that heavy bodies fall faster than light bodies)
(If tie two bodies together, they should fall faster because combination is heavier than heavy body)
Salviati: … We infer therefore that large and small bodies move with the same speed.
(The two tied together cannot fall both slower and faster than the heavy body alone)
Galileo apparently wrote about this question in dialogue format because he did not feel free to write directly explaining his views as he was already under house arrest for publishing a dialogue about whether the Earth was the center of the universe or revolved around the Sun.
In 1543, Nicolaus Copernicus (1473-1543) published De revolutionibus in which he proposed that the earth revolves around the sun rather than the sun around the earth.
Ninety years later, in 1632, Galileo published Dialogue on the Two Chief World Systems: Ptolemaic and Copernican. In 1633 Galileo was tried for heresy by the Holy Office of the Inquisition of the Catholic Church; Dialogue was prohibited. Galileo was forced to recant his claim that the Earth was not the center of the universe, which he had claimed based on his observations with a telescope that the moons of the planet Jupiter revolved around Jupiter. He had used these observations to support his claim that the Earth moved around the Sun. He was placed under life-long house arrest. In 1638, his Dialogue Concerning Two New Sciences was published in Holland. He died in 1642.
In 1979, Pope John Paul II called for theologians, scholars, historians, to reexamine Galileo’s case. In 1992, Pope John Paul II publicly endorsed Galileo’s support of the Copernican system, that the Earth revolves around the sun (http://www.accademiascienze.va/content/accademia/en/magisterium/johnpaulii/31october1992.html and http://www.baskent.edu.tr/~tkaracay/etudio/agora/news/Galileo.html ).
For information about Galileo’s life see: https://plato.stanford.edu/entries/galileo/
For a fascinating story based on Galileo’s daughter’s letters to him, which have survived and are located at the National Central Library of Florence Italy, see:
Sovel, D. (1999). Galileo’s daughter: A historical memoir of science, faith, and love. New York: Penguin Books.
3. Modeling Galileo’s exploration of falling objects
- Place two small objects with same shape but different masses on a board
- Place a pad (rug or cardboard) on the floor
- Hold the board high above the pad
- Turn on a video camera focused on the pad
- Tip the board so the two objects start falling at the same time from the same height
- Listen (and watch) to see if they hit at different or the same time
- What do you observe?
Question 5.54 Why do light and heavy objects fall the way they do?
- Place both blocks on a table top:
Invite each member of the group to push both blocks at the same time
- Which block is harder to get moving? Why?
The inference is that although the Earth pulls harder on the heavier object, the heavier object is also harder to get going; it has a bigger inertia. This means that the objects accelerate at the same rate when falling toward the Earth as long as they do not encounter differences from air resistance as they fall. A person with a parachute falls slower that the person would without a parachute, for example, because of the role of air resistance in slowing the parachute’s fall.
Note that Sir Isaac Newton was apparently sitting under an apple tree while admiring a moon in the sky. He is said to have had the insight there that the moon was “falling” toward the earth in the same way that an apple from the tree was falling to the Earth, both being pulled toward the center of the Earth by a gravitational force by the Earth. As shown in Fig. 5.96, an object shot out of a canon at various velocities might fall to the Earth near the canon, fall farther from the canon, ‘fall’ into a circular orbit around the Earth, ‘fall’ into an elliptical orbit around the Earth, or ‘fall’ away from the Earth into space.(http://www.thestargarden.co.uk/Newtons-theory-of-gravity.html)
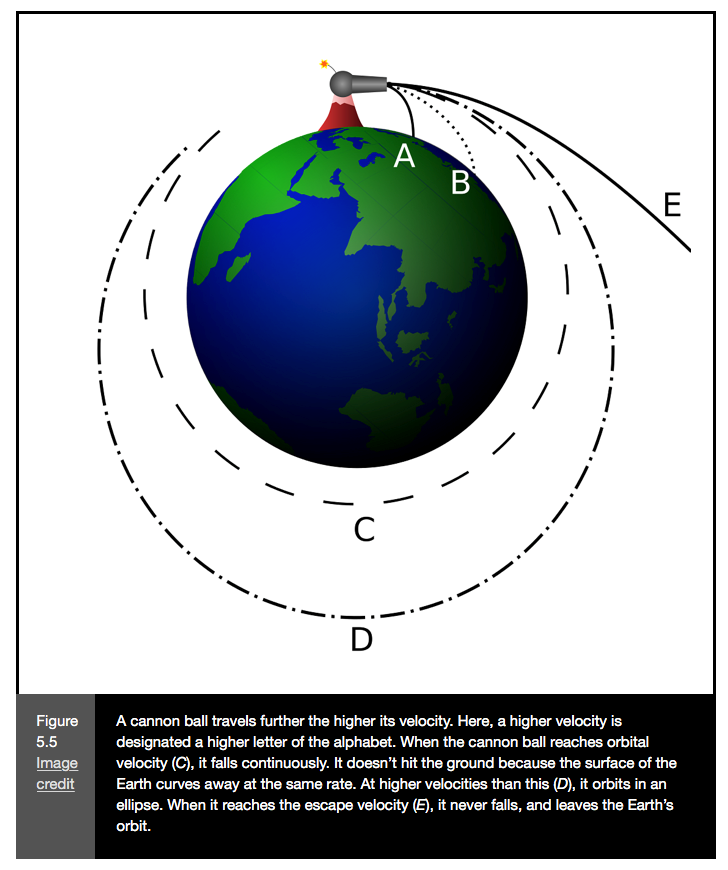
http://www.thestargarden.co.uk/Newtons-theory-of-gravity.html
Brian Brondel, https://commons.wikimedia.org/wiki/File:Newton_Cannon.svg. Licensed under an Attribution-ShareAlike 4.0 International (CC BY-SA 4.0) license, https://creativecommons.org/licenses/by-sa/4.0/.
Question 5.55 What happens when heavy and light objects drop from the same height at the same time on the moon?
- Watch astronauts dropping a hammer and a feather on the moon at https://www.youtube.com/watch?v=5C5_dOEyAfk
- What did they observe?
• Complete entries in Table V.16. Then write a summary of what you have learned about the role of gravitational forces in the Sun/Earth/Moon system.
Exploring the Role of Gravitational Forces in the Sun/Earth/Moon System
| Table V.16 Developing Additional Central Ideas about the Sun/Earth/Moon System | |||
|---|---|---|---|
| URL | Sketch of set up Evidence | Central Ideas | Vocabulary |
| https://theory.uwinnipeg.ca/ mod_tech/node24.html |
When two objects interact, each exerts an equal but opposite force on the other. | Newton’s Third Law | |
| http://www.physics.uwyo.edu/~davec/ teaching/Astro1050Summer2013/10_Newton.pdf |
A gravitational force is exerted by one mass on another mass that depends on the size of the masses and the square of the distance between them:
F = GMm/r2 |
Newton’s Universal Law of Gravitation | |
| http://scienceline.ucsb.edu/getkey.php?key=770 | When one object is revolving around another, the gravitational force by the larger object on the smaller object is keeping the smaller object in its orbit. | ||
| http://earthsky.org/earth/tides-and- the-pull-of-the-moon-and-sun http://oceanservice.noaa.gov/education/ kits/tides/tides06_variations.html |
Gravitational forces from the Moon and Sun influence the ocean’s tides on Earth | ||
| http://galileo.rice.edu/sci/ theories/on_motion.html |
Light objects and heavy objects speed up at the same rate as they fall near the surface of the Earth. | Aristotle
Galileo inertia |
|
| https://www.youtube.com/watch?v=5C5_dOEyAfk http://nssdc.gsfc.nasa.gov/planetary/lunar/ apollo_15_feather_drop.html |
Light objects and heavy objects speed up at the same rate when falling near the surface of the Moon. | ||
- Diagram arrangements of the Sun/Earth/Moon system that influence tides on Earth:
Highest and lowest tides Smallest tidal effects
4. Interpreting first grade students’ thoughts about falling objects
Question 5.55 What ideas do first grade students have about falling objects?
- Read and discuss Jamie Mikeska’s reflection upon engaging first grade students in exploring falling objects.
J. Mikeska, “First graders discuss dropping a book and a piece of paper,” In Seeing the science in children’s thinking, edited by D. Hammer and E. H. van Zee (Heinemann, Portsmouth, NH, 2006), pp. 71-83.
References
J. Mikeska, “First graders discuss dropping a book and a piece of paper,” In Seeing the science in children’s thinking, edited by D. Hammer and E. H. van Zee (Heinemann, Portsmouth, NH, 2006), pp. 71-83.
I. Newton, The mathematical principles of natural philosopy. Translated into English by Andrew Motte (London: Printed for Benjamin Motte, at the Middle-Temple-Gate in Fleetstreet, 1729). https://books.google.com/books?id=Tm0FAAAAQAAJ&printsec=frontcover&dq=Newton+mathematical+principles+Motte&lr=&as_drrb_is=b&as_minm_is=12&as_miny_is=1720&as_maxm_is=12&as_maxy_is=1800&num=20&as_brr=3#v=onepage&q=Newton%20mathematical%20principles%20Motte&f=false
P. P. Urone, R. Hinrichs, K. Dirks, and M. Sharma, College Physics. ( https://openstax.org/books/college-physics/pages/4-8-extended-topic-the-four-basic-forces-an-introduction and https://openstax.org/books/college-physics/pages/6-5-newtons-universal-law-of-gravitation )

