Unit 4: Considering the Influence of Light and Thermal Phenomena on Global Climate
III. Developing Central Ideas Based on Evidence
When light from the Sun shines on a person, the person feels warmer; when light from the Sun shines on a closed car, the seats, dashboard, steeling wheel, and air inside the car get warmer; when light from the Sun shines on a greenhouse in a garden, the plants, soil, and air inside the greenhouse get warmer.
What happens when light from the Sun shines on the atmosphere, land, and oceans of the Earth? Discussions about a warming Earth often refer to the greenhouse effect. To understand what is happening in the greenhouse effect on the entire Earth, we first need to review some of the central ideas developed in earlier units and to develop some additional central ideas about light and thermal phenomena.
A. Developing additional central ideas about light phenomena
Unit 1 developed the central idea that light can be envisioned as rays traveling in straight lines. As shown in Fig. 4.1, this was useful in drawing ray diagrams to explain the upside-down projection in a pinhole camera. Such ray diagrams also were useful to explain the apparent rise of a dot on the inside of a cup when the cup is filled with water as well as the appearance of rainbows in the sky.

Sometimes sunlight shining through clouds looks like rays of light, often informally called sunbeams and known as crepuscular rays (http://www.atoptics.co.uk/atoptics/ray1.htm). Children typically draw pictures of a sun with bright rays shining out in all directions. However, can you actually see rays of light traveling from various objects straight to your eyes?
Question 4.3 Are rays of light visible or invisible?
- Discuss with your group members in what sense you think light rays are visible or not.
When a driver sees a traffic light turn bright green, light must be traveling from the bulb to the driver’s eyes but the light rays’ journeys are not visible. Are there other experiences in which you can detect something even though its journey is not visible? When standing near an oven, for example, you can see the oven but how do you know whether the oven is “on” or not?
Question 4.4 What is “invisible light”?
If you are standing near an oven that is cooking dinner, you likely are aware the oven is on because you can feel its warmth. How is that energy getting to you? The oven is radiating energy even though you cannot see that energy is leaving the oven and traveling to your body. This process is called energy transfer by thermal radiation. You too are warm and radiating energy!
Equipment: If you have access to a thermal camera or to a computer with a “thermal camera” effect:
- What do think you will see in a thermal camera? Which areas of someone’s face, for example, might appear to be brighter than other areas when viewed through a thermal camera?
All objects radiate energy. Thermal cameras detect thermal radiation and represent it on the camera screen with varying levels of brightness that indicate varying levels of temperature as shown in Fig. 4.2.
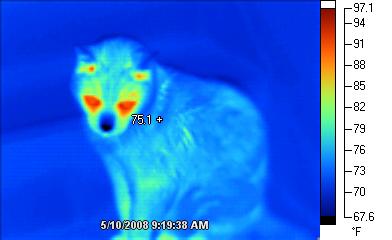
Sometimes called night-vision cameras, thermal cameras are helpful for “seeing” warm bodies in the dark or in smoky settings such as houses on fire. Thermal cameras have many uses in safety, law enforcement, healthcare, electronics, and maintenance. For information about various ways to use such cameras, search the Internet for “uses of thermal cameras” and view a website such as https://reductionrevolution.com.au/blogs/news-reviews/69333381-over-60-unexpected-uses-of-infrared-thermal-imaging-camera-images .
Thermal radiation also is known as infrared radiation. Some telescopes can “see” infrared radiation emitted by astronomical phenomena. Visible light images and infrared images look very different, as shown in Fig. 4.3. Both of these images are of the constellation known as Orion, the Hunter (https://in-the-sky.org/data/constellation.php?id=61). This constellation is visible in both northern and southern hemisphere skies.

On the left image, the light green lines connect the stars outlining the envisioned hunter’s shoulders, belt, and knees; a sword seems to hang below the belt. Within the blade of the hockey-stick figure is a giant cloud of dust, gas, and young stars known as the Orion nebula. This region of active star formation may be faintly visible on a clear dark night away from city lights. (See: https://www.nasa.gov/feature/goddard/2017/messier-42-the-orion-nebula). The constellation’s dusty clouds are vividly visible, however, in the infrared image on the right.
Infrared radiation is part of the electromagnetic spectrum. Your eyes cannot see infrared radiation but your skin can detect it as warmth. Light that you can see when light shines onto the retinas of your eyes is called visible light and consists of white light and its component colors. As shown in Fig. 4.4, however, visible light is only a small part of the electromagnetic spectrum.
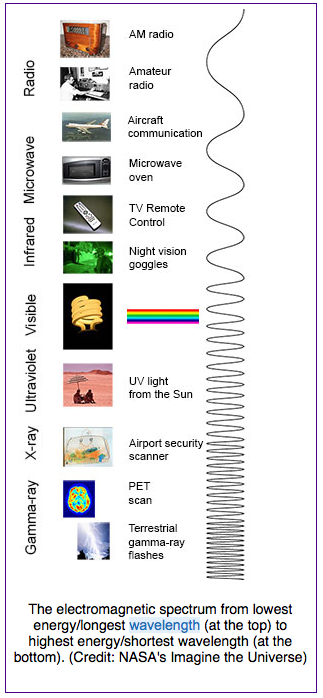
https://imagine.gsfc.nasa.gov/science/toolbox/emspectrum1.html
Although the names used in the electromagnetic spectrum refer both to rays (infrared radiation, ultra violet radiation, x-rays, gamma rays) and to waves (microwaves, radio waves), all of these forms of light can be described as waves, with varying wavelengths, as shown in Fig. 4.4. They also have varying frequencies, the number of waves that pass a point each second.
Fig. 4.5 illustrates the meaning of wavelength, the distance from one crest to the next, from one midpoint to the next, or from one trough to the next of a wave. The Greek letter lambda, λ, is typically used as the symbol to represent wavelength.
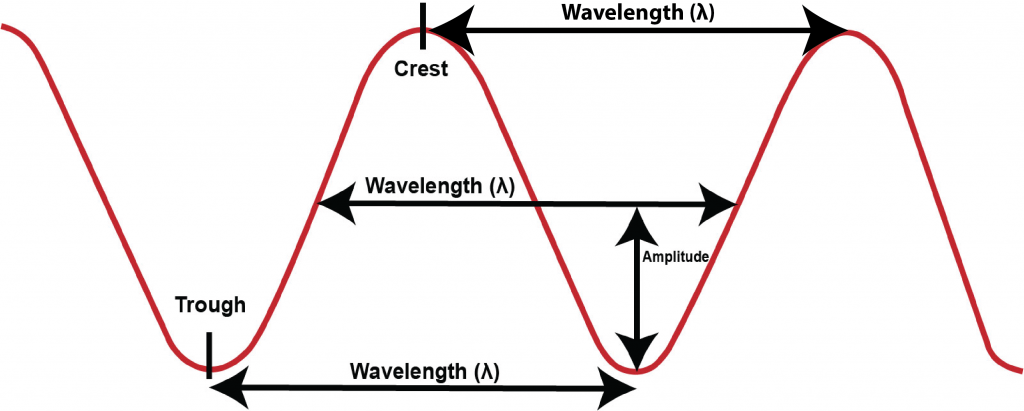
Forms of light with larger wavelengths than visible light are known as infrared radiation, microwaves, and radio waves. Forms of light with smaller wavelengths than visible light are known as ultra violet radiation, x-rays, and gamma rays. Radio waves have the largest wavelengths but the lowest frequencies and lowest energies. Gamma rays have the smallest wavelengths but the highest frequencies and energies.
Exploring the wave model of light
Equipment: Use a Slinky® for each pair of students
-
- With a partner, hold an end of a Slinky® with the Slinky® stretched out along the floor. What happens when one person gives the Slinky® a quick jerk side to side? These waves are similar to the s-waves that travel through the earth during an earthquake (see Fig. 3.24 in Unit 3).
- For more information about the electromagnetic spectrum, search on the Internet and read one of the many relevant websites, such as http://earthsky.org/space/what-is-the-electromagnetic-spectrum and
https://hubblesite.org/contents/articles/the-electromagnetic-spectrum
.
- To learn more about infrared radiation, watch Infrared: More Than Your Eyes Can See (6:45 min), with astrophysicist Dr. Michelle Thaller, from NASA’s Spitzer Space Telescope, at https://www.youtube.com/watch?v=v4J56lnl1UE&feature=emb_title
- Watch carefully what happens when Dr. Thaller demonstrates differences in the way that different materials transmit white light and infrared radiation:
- What happens when she puts her hands inside a black plastic bag when viewed with a regular camera? With an infrared camera?
- What happens when she brings a clear pane of glass near her face when viewed with a regular camera? With an infrared camera?
• The clear glass pane and black plastic bag differ in the property of transmissivity, how they transmit different forms of light. This black plastic bag transmits infrared but not visible light. This clear pane of glass transmits visible light but not infrared.
https://herschel.jpl.nasa.gov/farIRandSubmm.shtml. The Herschel Space Observatory is named after William Herschel, who was the first to notice this invisible form of light.
- Complete entries in Table IV.1. Then write a summary of what you have learned before reading an example of student work about visible light and infrared radiation.
| TABLE IV.1 Central ideas about the influence of light and thermal phenomena on global climate | |||
|---|---|---|---|
| URL/Sketch of set up | Evidence | Central Ideas | Relevant Vocabulary |
| https://hubblesite.org/contents/articles/the-electromagnetic-spectrum | Visible light and infrared radiation can be represented as waves and are part of a broad spectrum of such waves. | Electromagnetic spectrum
Infrared radiation |
|
| https://science.nasa.gov/ems/07_infraredwaves
http://www.youtube.com/watch?v=2–0q0XlQJ0 |
Hot objects emit energy as infrared radiation. | Emissivity | |
| http://www.youtube.com/watch?v=2–0q0XlQJ0 (Dr. Thaller) |
Materials differ in how much visible light and infrared radiation can pass through the material or are blocked. | Properties of materials: transmissivity reflectivity absorptivity |
|
1. Example of student work about visible light and infrared radiation.
Many of us have experienced the heat of the sun, as light shines on Earth and heats up the surface. We have noticed that sidewalks are hot on a sunny day, and that a car with the windows rolled up is hotter than a car with the windows rolled down.
Table (IV.1) features ideas explored in this lab about the influence of light and thermal phenomena on global climate.
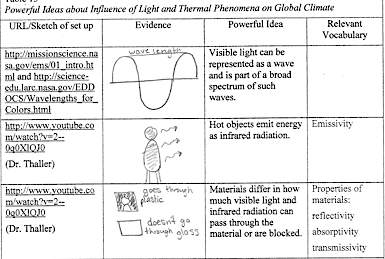
In row 1, the student drew a picture of a wave and a half wave and identified a wave length as extending from one crest to the next.
In row 2, the student drew a person with arrows representing infrared radiation emitted from the person’s body.
In row 3, the student drew a black plastic bag and wrote goes through plastic; the student also drew a glass pane and wrote doesn’t go through glass.
The student wrote the following rationales for the ideas claimed in the third column of the table:
Visible light can be represented as a wave and is part of a broad spectrum of such waves. In this lab we stretched our perception of light, envisioning it as moving in waves. The wave still travels in a straight line, which is the midpoint of the wave. The distance between each crest is the wavelength. The height of a wave is called amplitude, and frequency is how often the wave crest passes a point each second. Light waves emitted by the sun come in various wavelengths, which create the electromagnetic spectrum. Waves are classified by their wavelengths. The shortest waves are gamma rays, then x-rays, then UV rays. The visible light is what the human eye can see. The next largest wavelength is microwaves, and then radio waves have the largest wavelength on the spectrum.
Hot objects emit energy as infrared radiation. Dr. Michelle Thaller, http://www.youtube.com/watch?v=2–0q0XlQJ0, introduces the idea that, “Everything in the universe emits some kind of light.” Infrared radiation is a kind of light wave that is not visible to the human eye. Dr. Thaller provides many examples of infrared cameras, which measure the energy being emitted by an object, or temperature. Warmer objects look bright in infrared, because they are giving off more infrared radiation. Colder objects look dark because they are giving off less infrared radiation.
Materials differ in whether visible light and infrared radiation can pass through the material or are blocked. Dr. Michelle Thaller introduces the idea that visible light and infrared light pass through and are blocked by different materials. Infrared radiation can often pass through things that visual light cannot, such as a black plastic bag. Infrared also gets stopped by something visible light gets through, such as clear glass.
Physics student, Spring 2016
The history of the development of knowledge about various forms of “invisible light” is an example of the way that science develops, with participation and different points of view expressed and explored by a variety of individuals in many countries over several centuries (1600 to present day). To broaden your understanding, read about the discovery of infrared radiation as well as discoveries of the other forms of invisible light in the electromagnetic spectrum. The following two sections (III.A.2 and 3) provide a glimpse of this journey if the reader has time and interest. Otherwise proceed to Section III.B below.
2. Discovery of infrared radiation
In 1672, in England, Sir Isaac Newton published in the Philosophical Transactions of the Royal Society of London a paper about his new theory about light and colors and the experiments that supported his claims. (See Unit 1, IX.) He was curious what happens when light from the Sun shines through a prism and found that the light separated into a spectrum of colors, with each color bending as it entered a prism at its own angle of refraction. In 1704, he explained in detail his many experiments with white light and its component colors in a book, Opticks.
About a century later, an astronomer in England, Sir William Herschel (1800 a, b, c, d) reported his discovery of the invisible rays of the Sun in a series of papers he also published in the Philosophical Transactions of the Royal Society of London. What did Herschel mean by the “invisible rays of the Sun”?
Herschel was interested in the Sun as well as in the stars. To study the Sun during the day, he used different colored filters on his telescope to reduce the sunlight’s intensity. Some colored filters seemed to warm his eye more than others and he became curious about this uncomfortable effect.
To explore how the different colors in the spectrum warmed a material, Herschel placed a prism in a window and oriented it to make a spectrum of red, orange, yellow, green, blue, and violet light shine on a table. As Newton had observed about 100 years earlier, the red light rays were bent the least by the prism and violet the most (see Unit 1, IX). Herschel, however, was asking a different question, about how light of different colors warmed materials.
As shown in Fig. 4.7, Herschel used three thermometers: thermometer #1 measured changes in temperature when its bulb was placed within a band of color in the spectrum on the table; thermometers #2 and #3 served as controls when placed nearby but outside the spectrum.
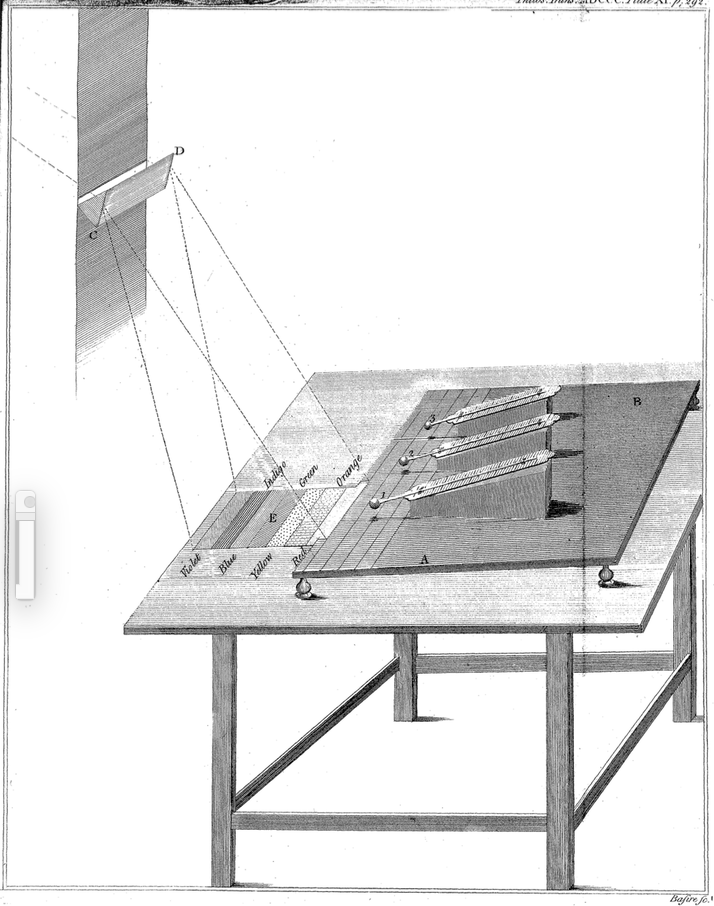
http://rstl.royalsocietypublishing.org/content/90/284.full.pdf+html, p. 292.
Herschel was surprised that thermometer (#1) warmed up when he placed it just beyond the red band of the visible spectrum. It warmed even though no light appeared to be shining on it! Like Newton, Herschel referred to the refraction of light rays by the prism as refrangibility. After reporting details of his experimental setup and data collected, Herschel concluded:
The first four experiments prove that there are rays coming from the sun, which are less refrangible than any of those that affect the sight. They are invested with a high power of heating bodies, but with none of illuminating objects; and this explains the reason why they have hitherto escaped unnoticed.
Herschel, 1800b, p. 290
These were invisible rays of the Sun because they could heat an object without appearing to shine on the object, illuminating it. These invisible rays were bent by the prism less than any of the colored rays, landing on the apparatus just beyond the red band of the visible spectrum.
Herschel also demonstrated that these invisible rays exhibited the same laws of reflection and refraction that were well known for white and colored light. He also studied similar effects for terrestrial rays such as from fires whose embers were no longer red hot but still warmed thermometers placed nearby.
This was the discovery of what is known as infrared radiation, energy that warms materials but does not make them visible to human eyes. This is an example of an unexpected finding during an exploration motivated by a practical need: Herschel wanted to understand why filters of different colors warmed his eye differently when he was looking at the Sun through his telescope. He was surprised when he noticed the increased temperature of the thermometer placed beyond the red band of the spectrum.
Herschel also had placed a thermometer beyond the violet band of the spectrum. Seeing little if any temperature change, however, he had concluded, “I was now sufficiently persuaded that no rays which might fall beyond the violet, could have any perceptible power, either of illuminating or heating” (Herschel, 1800b, p. 288).
- One way to explore infrared radiation is to replicate Herschel’s experiment. See, for example, https://coolcosmos.ipac.caltech.edu/page/lesson_herschel_experiment . This experiment uses a glass prism, several identical thermometers, a way to hold the prism still, a white sheet of paper, a box, and a sunny day.
- See https://www.youtube.com/watch?v=zmiU5tJRJd4 for an introduction to infrared radiation and a demonstration of this experiment.
- Neil deGrasse Tyson, an astrophysicist who is director of the Hayden Planetarium, has described “the brilliant way that infrared light was discovered” at https://www.youtube.com/watch?v=Pr4qEhcGPq8.
Herschel and his sister Caroline became world famous for their surveys of the skies with telescopes made and used in their home. Among Caroline Herschel’s achievements were the discovery of three nebulae and eight comets as well as development of an extensive catalogue of stars and nebulae (https://www.skyandtelescope.com/observing/in-caroline-herschels-footsteps; https://mathshistory.st-andrews.ac.uk/Biographies/Herschel_Caroline/ . In 1828, she was the first woman to be awarded a Gold Medal of the Royal Astronomical Society (https://www.esa.int/Science_Exploration/Space_Science/Herschel/Caroline_and_William_Herschel_Revealing_the_invisible).
Herschel’s papers and Newton’s 1672 paper in the Philosophical Transactions of the Royal Society of London are available online as is Newton’s Opticks:
Herschel, W. (1800a). Investigation of the powers of the prismatic colours to heat and illuminate objects; with remarks, that prove the different refrangibility of radiant heat. To which is added, an inquiry into the method of viewing the sun advantageously, with telescopes of large apertures and high magnifying powers. Philosophical Transactions of the Royal Society of London 90, 255-283. http://rstl.royalsocietypublishing.org/content/90/255.full.pdf+html
Herschel, W. (1800b). Experiments on the refrangibility of the invisible rays of the sun. Philosophical Transactions of the Royal Society of London 90, 284-292. http://rstl.royalsocietypublishing.org/content/90/284.full.pdf+html
Herschel, W. (1800c). Experiments on the solar, and the terrestrial rays that occasion heat; with a comparative view of the laws to which light and heat, or rather the rays which occasion them, are subject, in order to determine whether they are the same, or different. Part I. Philosophical Transactions of the Royal Society of London 90, 293-326. http://rstl.royalsocietypublishing.org/content/90/293.full.pdf+html
Herschel, W. (1880d). Experiments on the solar, and the terrestrial rays that occasion heat; with a comparative view of the laws to which light and heat, or rather the rays which occasion them, are subject, in order to determine whether they are the same, or different. Part II. Philosophical Transactions of the Royal Society of London 90, 437-538. http://rstl.royalsocietypublishing.org/content/90/437.full.pdf+html
Newton, I. (1672). A letter of Mr. Isaac Newton, Professor of the Mathematics in the University of Cambridge; Containing his new theory about light and colors: Sent by the author to the publisher from Cambridge, Febr. 1671/72; in order to be communicated to the R. Society. Philosophical Transactions of the Royal Society of London, 6, (60-80) 3075-3087. https://royalsocietypublishing.org/doi/pdf/10.1098/rstl.1671.0072
Newton, I. (1704). Opticks: Or a treatise of the reflections, refractions, inflections and colours of light. London: Printed for Sam. Smith and Benj. Walford. Printers to the Royal Society. http://www.gutenberg.org/files/33504/33504-h/33504-h.htm
3. Discoveries of the other invisible portions of the electromagnetic spectrum
Discovery of the rest of the invisible portion of the electromagnetic spectrum occurred during the next hundred years, 1800-1900. A German scientist, Johann Wilhelm Ritter, was aware of Herschel’s discovery of invisible rays beyond the red band in the spectrum of visible light and decided to check for himself whether there were invisible rays beyond the violet band.
Ritter had been experimenting with a chemical, silver chloride, that darkened when placed in sunlight. In 1801 he found that this chemical reacted very little when placed in the red band of the spectrum, darkened when placed in the blue band, and reacted intensely when placed beyond the violet band in the spectrum, demonstrating the presence of an invisible form of light there also. He attributed this effect to chemical rays, which later were called ultraviolet radiation (see: https://www.britannica.com/biography/Johann-Wilhelm-Ritter .)
A hundred years earlier, Newton and Huygens had disagreed about whether light should be envisioned as rays, made up of particles traveling in straight lines, or as waves, traveling in spreading circles. This discussion continued with Herschel writing in terms of rays and a contemporary, Thomas Young, writing in terms of waves.
Herschel described his findings in terms of invisible rays of the Sun that were reflected and refracted in the same way as white light and the colors of the visible spectrum. Young, however, envisioned light as undulations that spread out from a source in expanding waves, like sound waves and water waves when a pebble is dropped in a puddle. In an article published in 1802 in the Philosophical Transactions of the Royal Society of London, Young used a wave model of light to explain findings from a double-slit experiment, in which light passing through two slits created interference patterns on a screen (see: http://micro.magnet.fsu.edu/primer/java/interference/doubleslit/.)
Young, T. (1802). The Bakerian Lecture: On the Theory of Light and Colours. Philosophical Transactions of the Royal Society of London, 92, 12-48.
http://rstl.royalsocietypublishing.org/content/92/12.full.pdf+html
More than sixty years passed before a Scottish scientist, James Clerk Maxwell predicted the existence of other forms of electromagnetic waves in his theoretical article, A dynamical theory of the electromagnetic field, published in 1865 in the Philosophical Transactions of the Royal Society of London (see: https://science.hq.nasa.gov/kids/imagers/ems/consider.html ).
Maxwell, J. C. (1865). A dynamical theory of the electromagnetic field. Philosophical Transactions of the Royal Society of London, 155, 459-512. http://rstl.royalsocietypublishing.org/content/155/459.full.pdf+html
In 1888, a German scientist, Heinrich Hertz, designed ways to produce and study radio waves and microwaves experimentally (http://www.sparkmuseum.com/BOOK_HERTZ.HTM). [Percy Spencer, an American scientist, invented the microwave oven in 1946 after noticing that something had melted in his pocket one day as he was working on improving radar technology (http://www.popularmechanics.com/technology/gadgets/a19567/how-the-microwave-was-invented-by-accident/ .]
A German scientist, William Roentgen, received the first Noble Prize in Physics, in 1901, for discovering X-rays in 1895. He named these new puzzling rays after the “x” representing unknowns in mathematics (https://www.nobelprize.org/nobel_prizes/physics/laureates/1901/rontgen-bio.html)
A French scientist, Paul Villard, discovered gamma rays in 1900. Gamma rays are generated by radioactive atoms (https://link.springer.com/article/10.1007/s000160050028). He was using a radioactive sample he had been given by a Paris colleague, Marie Curie. She won the Nobel Prize twice, in 1903 and 1911, for her studies of radioactivity https://www.nobelprize.org/nobel_prizes/physics/laureates/1903/marie-curie-facts.html )
The issue of what IS light continued to be discussed during the 20th century: is light a series of spreading waves or is light a stream of particles moving in straight lines? In 1905, Albert Einstein wrote:
Indeed, it seems to be that…the production or conversion of light can be understood better if one assumes that the energy of light is discontinuously distributed in space. According to the assumption to be contemplated here, when a light ray is spreading from a point, the energy is not distributed continuously over ever-increasing spaces, but consists of a finite number of energy quanta that are localized in points in space, move without dividing, and can be absorbed or generated only as a whole.
Einstein, A. (1905). On a heuristic point of view concerning the production and transformation of light. Annelen der Physik 17: 132-148. (translated from the German by Dr. Anna Beck and Professor Peter Havas in The Collected Papers of Albert Einstein Volume 2: The Swiss Years: Writings, 1900-1909, p. 87 (http://einsteinpapers.press.princeton.edu/vol2-trans/101 ) Princeton University Press.
Einstein received the Nobel Prize in 1922 for this paper, in which he explained the photoelectric effect in terms of particles of light, now known as photons. A series of Nobel Prizes were awarded during the 20th century for theorists and experimentalists exploring the wave and particle natures of both light and matter as inferred in the context of quantum mechanics. See https://www.nobelprize.org/nobel_prizes/themes/physics/ekspong/ for the story of evolving understandings about the wave-particle duality of light and matter.
See https://ocw.mit.edu/courses/5-111sc-principles-of-chemical-science-fall-2014/pages/unit-i-the-atom/lecture-3/ for a recent lecture about the Wave-Particle Duality of Light in an open source course at the Massachusetts Institute of Technology by Professor Catherine Drennen (https://drennan.mit.edu/education/group-members/catherine-l-drennan/) and (http://dyslexiahelp.umich.edu/success-stories/catherine-drennan ). Her lecture on the Wave-Particle Duality of Matter and the Schrodinger Equation is available at https://ocw.mit.edu/courses/5-111sc-principles-of-chemical-science-fall-2014/pages/unit-i-the-atom/lecture-4/.
Professor Lisa Randall (https://www.physics.harvard.edu/people/facpages/randall), a theoretical physicist at Harvard University, has written about the wave-particle duality in terms of the level at which one is looking, whether one is using one’s eyes looking at everyday things or “looking” at an atomic level where quantum mechanical effects occur. The phrase classical refers to physics understandings in the everyday world. The phrase quantum mechanical refers to physics understandings at the level of and within atoms and molecules.
…none of us (with the possible exception of superheroes) sees individual photons, so quantum mechanical effects cannot be easily detected. Ordinary light doesn’t look as if it’s made up of quanta. We see bunches of photons that constitute visible light. The large number of photons together act as a classical wave.
You need a very weak source of photons, or a very carefully prepared system, to observe the quantized nature of light. When there are too many photons, you can’t distinguish the effect of any single one. Adding one more photon to classical light, which contains many photons, just doesn’t make a big enough difference. If your lightbulb, which behaves classically, emitted one additional photon, you would never notice. You can observe detailed quantum phenomena only in carefully prepared systems.
Randall, L. (2005). Warped passages: Unraveling the mysteries of the universe’s hidden dimensions. New York: Harper Collins, p. 136-137.
B. Reviewing central ideas about thermal phenomena developed in earlier units
Units 2 and 3 developed some central ideas about how energy flows from one place to another. These ideas are relevant in exploring what happens when light from the Sun shines on the Earth.
Question 4.5 How does energy flow from one place to another?
Energy transfer processes include transmission, reflection, absorption, emission, conduction, convection, melting, freezing, sublimation, transpiration, evaporation, and condensation. Properties of materials such as specific heat, thermal conductivity, and reflectivity also affect what happens when energy flows from one place to another such as on a sunny day at the beach when the sand is hot, the water cool, and a cloudy sky as well as sea breezes often occur in the afternoon (Unit 3, V. Questions 3.8 and 3.9). Tracing the flow of energy in this scenario involved interpreting a diagram as shown in Fig. 3.9 and repeated as Fig. 4.8 below.
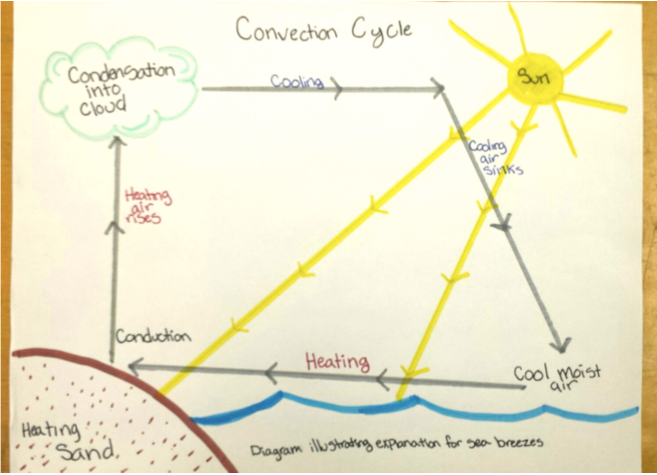
The explanation of sea breezes included the following story about how energy flows from the Sun and circulates around the sand, water, and atmospheric system during a sunny day at the beach:
The Sun radiates energy to the Earth.
Some of the energy is reflected by the sand and the water
Some of the energy is absorbed by the sand and the water.
Sand and water differ in the property of specific heat. One gram of water needs about five times as much energy as one gram of sand to change temperature by one degree C. This means that if equal masses of sand and water absorb the same amount of energy, the sand’s temperature will increase about 5 times as much as the water’s temperature increases.
Sand and water also differ in the property of thermal conductivity. Sand’s thermal conductivity is low; this means that energy absorbed by the sand stays near the surface of the sand; sand below the surface remains cool. Water’s thermal conductivity is high; this means that energy absorbed by the water at the surface spreads throughout the water; water below the surface warms along with the water at the surface.
Because energy absorbed stays near the surface of the sand and less energy is needed to increase the sand’s temperature, sand gets hot. Because energy absorbed spreads throughout the water and more energy is needed to increase the water’s temperature, the water stays cool even though the sun has been shining on both sand and water in the same way for the same time.
Sand and water also differ in the property of reflectivity. Sand reflects up to 40% of incoming sunlight depending upon its composition whereas liquid water reflects only about 6% unless the Sun is close to the horizon. However, this difference is masked by the large difference in specific heats. Even if a gram of water absorbed an entire calorie of energy from the sun and a gram of sand reflected 40% of a calorie of energy from the sun, the sand would still warm up three times as much as the water.
Also some of the water evaporates into the air above the surface of the water. Evaporation uses energy to change water from a liquid to a gaseous form, so the energy from some of the light from the Sun shining on the water goes into this process rather than into warming the water.
Energy flows from hot objects to cold objects. When the objects are touching this process is called energy transfer by conduction. The hot sand warms the cool air above it by conduction.
Fluids expand when warmed. The warmed air, becoming less dense, rises into the cooler upper atmosphere; the warmed air cools as its energy flows into the cooler surrounding air; cool more dense air sinks back toward the surface. This process is called energy transfer by convection.
As the warm air rises, moist cool air over the water forms a sea breeze by flowing toward the land. The hot sand warms the moist air; the warmed moist air becomes less dense and rises into the cooler upper atmosphere; the warmed moist air cools as its energy flows into the cooler surrounding air; as the moist air cools, the moisture condenses into water droplets, forming clouds; this releases some energy into the upper atmosphere as the water changes back from a gaseous to liquid form; this energy may get dissipated during storms as wind, thunder, and lighting; the cool more dense air sinks back toward the surface.
This complex process of tracing the energy from the Sun as it flows from one place to another is useful preparation for thinking about happens when the Sun shines not only on the sand and water at a beach but on the entire Earth.
Question 4.6 What is the role of systems thinking in understanding the Earth’s energy budget?
In Unit 2, Question 2.10, it was important to think about the system involved when comparing the ratio of masses of hot and cold water to the ratio of their changes in temperature when mixed together. Was all the energy lost by the hot water flowing into the cold water or was some energy flowing into the containers or nearby air? To completely account for all of the energy lost by the hot water, one needed to think what was happening to the energy in the entire system, not only in the cups of hot and cold water but also in their surroundings.
In this unit, the system of interest includes the entire Earth. What is happening to the energy that the Sun is radiating to the Earth? Is the amount of energy radiated to Earth from the Sun also the same as the amount of energy flowing away from the Earth into space? The balance between energy flowing in and out is referred to as the Earth’s energy budget in analogy to a financial budget that monitors the balance between income and expenses.
For a system to be in thermal equilibrium, the amount of energy leaving the system must equal the amount of energy entering the system. This central idea underlies the influence of light and thermal phenomena on global climate and in particular, the phenomenon known as the greenhouse effect.
- Complete entries in the continuation of Table IV.1
| TABLE IV.1 Central ideas about the influence of light and thermal phenomena on global climate (continued) | |||
|---|---|---|---|
| URL/Sketch of set up | Evidence | Central Ideas | Relevant Vocabulary |
| Energy transfer occurs through a variety of processes. |
Radiation Reflection Absorption Emission of infrared radiation Transmission Conduction Convection Changes in State |
||
| http://earthobservatory.nasa .gov/Features/EnergyBalance /page4.php |
The Earth’s energy budget is the flow of incoming and outgoing energy. | System | |
Complete documenting your exploration and writing a summary before looking at an example of student work about energy transfer processes and the Earth’s energy budget.
1. Example of student work about energy transfer processes and the Earth’s energy budget.

In the first row, the student drew a picture of a hand touching a block (from Unit 2,III,A,Question 2.2) and wrote From our touch: The student also drew a picture of a light bulb and wrote From another source. The student also wrote, Energy transfer occurs through touch, and through emission.
In the second row, the student drew a half circle representing Earth and an arrow pointing in from the Sun, represented with a small circle, as well as an arrow pointing out from the large half circle representing Earth.
The student wrote the following rationales for the central ideas claimed in the third column of the table:
Energy transfer occurs through a variety of processes. Energy from the Sun is transferred through radiation – light rays traveling to an object – like sand, and transferring the energy, heating the sand. Reflection can block some energy from being transferred, such as the ocean reflecting radiation when the Sun is at an angle. The sand on the beach absorbs the Sun’s energy all along the top layer of the sand, heating it. Infrared radiation is emitted from warm objects, such as a person’s hand. An infrared camera can detect and display warm and cold regions based on the emission of infrared radiation. Conduction transfers energy through direct contact, such as a warm hand on a piece of metal. Convection is the energy transfer that can occur in fluids, when a heat source heats an area of water… The warm water rises and travels towards the cooler area, and the cool water sinks and travels towards the warmer area…An example of a change in state of water due to energy is evaporation. Sometimes sunlight provides enough energy for some of the liquid water in bodies of water to evaporate.
The Earth’s energy budget is the flow of incoming and outgoing energy. Through the processes of radiation, reflection, and absorption, energy enters and exits Earth’s atmosphere. For a stable environment, Earth’s incoming energy should be equal to Earth’s outgoing energy. If the budget is not balanced, the temperature within Earth’s atmosphere, oceans and land forms will change. If the incoming energy is greater than the outgoing energy, then the temperature will rise. If the outgoing energy is greater than the incoming energy, then the temperature will decrease. For stabile temperatures on Earth, the incoming and outgoing energy should be equal.
Physics student, Spring 2016
These central ideas about energy transfer processes and the concept of the Earth’s energy budget are key for understanding the greenhouse effect within the Earth’s climate system.

