8 Cost Curves
The Policy Question
Should the Federal Government Promote the Domestic Production of Streetcars?
In recent years, streetcars have enjoyed a bit of a renaissance in the United States. Streetcars are electric-powered public vehicles that ride on rails embedded into normal city streets and comingle with traffic. Once common in the United States and still common in many European cities, streetcars all but disappeared from US streets in the second half of the twentieth century. Portland, Oregon, is one city that revived the streetcar and subsequently expanded its system.
After initially buying streetcars from the German company Siemens, Portland’s transit authority and government, pushed by the federal government, which funds a large portion of urban transit projects, decided to contract with a local firm, Oregon Iron Works, to produce the streetcars locally. Oregon Iron Works had no experience in manufacturing streetcars but created a subsidiary firm to do so called United Streetcar. Other US cities that were introducing streetcars, such as Washington, DC, and Tucson, Arizona, contracted with Oregon Iron Works for their cars as well. In the end, the firm faced severe delays and cost overruns and eventually got very behind on its scheduled delivery. In addition, the expected boom in streetcars slowed considerably with the recession of 2008 and changing municipal priorities. In 2014, United Streetcar ceased production and laid off its workers.
Exploring the Policy Question
Is the story of United Streetcar an example of a misguided effort to steer business domestically? Would it have succeeded if the market for streetcars in the United States had not dried up? To answer these questions, we need to think about the cost structure of the industry and whether there are aspects of it that would support the decision to start manufacturing streetcars domestically. Cost curves—the subject of this chapter—are critical tools for analyzing a company’s cost structure.
Learning Objectives
8.1 Short-Run Cost Curves
Learning Objective 8.1: Derive the seven short-run cost curves from the total cost function.
8.2 Long-Run Cost Curves
Learning Objective 8.2: Derive the three long-run cost curves from the total cost function.
8.3 Short-Run versus Long-Run Costs: The Advantage of Flexibility
Learning Objective 8.3: Explain why long-run costs are always as low as or lower than short-run costs and how more flexibility in choosing inputs is always better than less.
8.4 Multiproduct Firms, Learning Curves, and Learning by Doing
Learning Objective 8.4: Explain how making more than one product, learning over time, and learning by producing can lower costs.
8.5 Policy Example
Should the Federal Government Promote Domestic Production of Streetcars?
Learning Objective 8.5: Use a cost analysis to explain why building streetcars domestically in the United States is or is not a good policy.
8.1 Short-Run Cost Curves
Learning Objective 8.1: Derive the seven short-run cost curves from the total cost function.
A cost curve represents the relationship between output and the different cost measures involved in producing the output. Cost curves are visual descriptions of the various costs of production. In order to maximize profits, firms need to know how costs vary with output, so cost curves are vital to the profit maximization decisions of firms.
There are two categories of cost curves: short run and long run. In this section, we focus on short-run cost curves.
The Seven Short-Run Cost Measures
The short run, as we learned in the previous chapter, is a time period short enough that some inputs are fixed while others are variable. There are seven cost curves in the short run: fixed cost, variable cost, total cost, average fixed cost, average variable cost, average total cost, and marginal cost.
The fixed cost ([latex]FC[/latex]) of production is the cost of production that does not vary with output level. The fixed cost is the cost of the fixed inputs in production, such as the cost of a machine (capital) that costs the same to operate no matter how much production is happening. An example of such a machine is a conveyor belt in a factory that moves a streetcar chassis through various stages of an assembly line. The belt is either on or off, but the cost of running it does not change depending on how many streetcars it carries at any point in time.
Note that the fixed cost of a piece of capital equipment that the company owns includes the opportunity cost as well. In our example, the fixed cost includes the actual costs of running the conveyer belt, such as power and maintenance, as well as the opportunity cost of using it for the firm’s own production rather than renting it out to another company.
The variable cost ([latex]VC[/latex]) of production is the cost of production that varies with output level. This is the cost of the variable inputs in production—for example, the cost of the workers that assemble the electronic devices along a conveyor belt. The number of workers might depend on how many devices the factory is trying to produce in a day. If its production target increases, it uses more labor. Thus the hourly wages it pays for these workers are a variable cost. Variable cost generally increases with the amount of output produced.
Like fixed cost of production, there is an opportunity cost associated with variable cost of production. In this case, the next best use of these workers is to go to another firm that will employ them. Thus the market wage for workers represents their opportunity cost, and as such, the wage cost of employing them is equivalent to their opportunity cost.
The total cost ([latex]C[/latex]) of production is the sum of fixed and variable costs of production:
[latex]C = FC + VC[/latex]
There are three short-run average cost measures: average variable cost, average fixed cost, and average total cost.
Average variable cost ([latex]AVC[/latex]) is the variable cost per unit of output. Mathematically, it is simply the variable cost divided by the output:
[latex]AVC = VC/Q[/latex]
Note that since variable cost generally increases with the amount of output produced, the average variable cost can increase or decrease as output increases.
Average fixed cost ([latex]AFC[/latex]) is the fixed cost per unit of output. Mathematically, it is simply the fixed cost divided by the output:
[latex]AFC = FC/Q[/latex]
Because fixed cost does not change with the amount of output produced, the average fixed cost always decreases as output increases.
Average total cost ([latex]AC[/latex]), or simply average cost, of production is total cost per unit of output. This is the same as the sum of the average fixed cost and the average variable cost:
[latex]AC = AC/Q = AFC + AVC[/latex]
Because it is the sum of the average fixed cost, which is always declining with output, and the average variable cost, which may increase or decrease with output, the average total cost may increase or decrease with output.
Marginal cost ([latex]MC[/latex]) is the additional cost incurred from the production of one more unit of output. Thus marginal cost is
[latex]MC=\frac{\Delta C}{\Delta Q}[/latex].
The only part of total cost that increases with an additional unit of output is the variable cost, so we can re-write the marginal cost as
[latex]MC=\frac{\Delta VC}{\Delta Q}[/latex].
Fixed Cost, Variable Cost, and Total Cost Curves
Table 8.1 summarizes a firm’s daily short-run costs. The firm has a fixed cost of $50 per day of production. This cost is incurred whether the firm produces or not, as we can see by the fact that $50 is still a cost when output is zero. The firm’s fixed cost of $50 does not change with the amount of output produced. The data in the first two columns of table 8.1 allow us to draw the firm’s fixed cost curve. It is a horizontal line at $50, as shown in figure 8.1.
| Table 8.1 An example of the seven short-run cost measures, organized by total cost per unit of output. | |||||||
|---|---|---|---|---|---|---|---|
| Output (variable Q) | Fixed cost (variable FC) | Variable cost (variable VC) | Total cost (variable C) | Marginal cost (variable MC) | Average fixed cost (variable AFC) | Average variable cost (variable AVC) | Average cost (variable AC) |
| When Output(Q) equals 0… | FC=50 | VC=0 | C=50 | MC=0 | AFC=0 | AVC=0 | AC=0 |
| When Output(Q) equals 1… | FC=50 | VC=40 | C=90 | MC=40 | AFC=50.0 | AVC=40.0 | AC=90.0 |
| When Output(Q) equals 2… | FC=50 | VC=70 | C=120 | MC=30 | AFC=25.0 | AVC=35.0 | AC=60.0 |
| When Output(Q) equals 3… | FC=50 | VC=90 | C=140 | MC=20 | AFC=16.7 | AVC=30.0 | AC=46.7 |
| When Output(Q) equals 4… | FC=50 | VC=100 | C=150 | MC=10 | AFC=12.5 | AVC=25.0 | AC=37.5 |
| When Output(Q) equals 5… | FC=50 | VC=120 | C=170 | MC=20 | AFC=10.0 | AVC=24.0 | AC=34.0 |
| When Output(Q) equals 6… | FC=50 | VC=150 | C=200 | MC=30 | AFC=8.3 | AVC=25.0 | AC=33.3 |
| When Output(Q) equals 7… | FC=50 | VC=190 | C=240 | MC=40 | AFC=7.1 | AVC=27.1 | AC=34.3 |
| When Output(Q) equals 8… | FC=50 | VC=240 | C=290 | MC=50 | AFC=6.3 | AVC=30.0 | AC=36.3 |
| When Output(Q) equals 9… | FC=50 | VC=300 | C=350 | MC=60 | AFC=5.6 | AVC=33.3 | AC=38.9 |
| When Output(Q) equals 10… | FC=50 | VC=370 | C=420 | MC=70 | AFC=5.0 | AVC=37.0 | AC=42.0 |
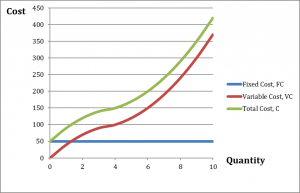
Figure 8.1 also shows variable and total cost curves plotted from data in table 8.1. The variable cost increases with output because extra output requires extra variable inputs. As we can see in the graph, the variable cost curve rises as output, [latex]Q[/latex], increases.
The short-run variable cost curve is determined by and matches the shape of the short-run production function, which we studied in chapter 6. The short-run production function is the same as the total product of labor curve when labor is the variable input in the short run, which we always assume it is. To go from the production function to the variable cost curve requires knowing the price of labor. Let’s assume a constant price of labor, say $10 an hour.
Figure 8.2 presents a typical short-run production function, which leads to the shape of the variable cost curve in figure 8.1. The production function exhibits increasing marginal returns to labor initially: as the labor input is increased from zero, the output increases at an increasing rate. Eventually, however, the addition of extra hours of labor leads to additional output at a decreasing rate. This happens as we increase labor input from ten hours of labor.
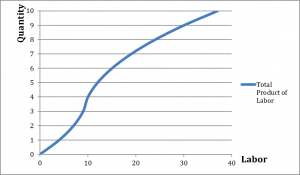
If we multiply the amount of labor at every level of output in figure 8.2 by the wage rate of $10 per hour, we get the variable cost curve from figure 8.1.
Marginal, Average Fixed, Average Variable, and Average Total Cost Curves
Figure 8.3 presents the four remaining short-run cost curves: marginal cost ([latex]MC[/latex]), average fixed cost ([latex]AFC[/latex]), average variable cost ([latex]AVC[/latex]), and average total cost ([latex]AC[/latex]).
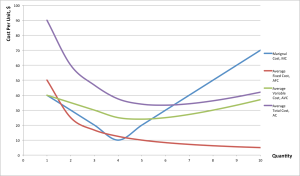
The marginal cost, average variable cost, and average total cost curves are derived from the total cost curve.
From figure 8.3, we can see that the marginal cost curve crosses both the average variable cost curve and the average fixed cost curve at their minimum points. This is not random. Since the marginal cost indicates the extra cost incurred from the production of the next unit of output, if this cost is lower than the average, it must be bringing the average down. If this cost is higher than the average, it must pull the average up. Think of your own grade point average: if your average this term is higher than your overall average, your overall average will go up. If your average this term is lower than your overall average, your overall average will go down.
Calculus
8.2 Long-Run Cost Curves
Learning Objective 8.2: Derive the three long-run cost curves from the total cost function.
As we learned in previous chapters, in the long run, all inputs are variable, and there are no fixed costs. In this section, we look at the three long-run cost curves—total cost, average cost, and marginal cost—and how to derive them.
Long-Run Total Cost Curve
To determine the long-run total cost (LRTC) for a firm, we must think about the cost minimization problem introduced in chapter 7. Remember that the cost minimization problem answers the question, What is the most cost-effective way to produce a given amount of output? The total cost curve represents the cost associated with every possible level of output, so if we figure out the cost-minimizing choice of inputs for every possible level of output, we can determine the cost of producing each level of output.
When we do this exercise, we are looking for the expansion path of the firm. Recall from chapter 7 that the expansion path is the combination of inputs that minimize costs for every level of output, and it can be graphed as a curve. Figure 8.4 shows the expansion path for a firm that manufactures tablet computers.
Each point on the expansion path is the solution to the cost minimization problem for that particular output. Recall from chapter 7 that [latex]r[/latex] is the rental rate or price of capital and [latex]w[/latex] is the wage rate or price of labor. Consider point X: here the output quantity is set at ten million, and the tangency of the isocost and isoquant at this point establishes the optimal combination of the inputs. To go from this point to the cost, we have only to know the combined cost of the inputs. Fortunately, the isocost line tells us exactly that; the total cost here is [latex]C_1[/latex]. Now consider point Y, where the output quantity has increased to twenty million. With this, the new production level is associated with a new isocost curve, with total cost at [latex]C_2[/latex]. Finally, point Z indicates that for an output quantity of thirty million, the total cost is [latex]C_3[/latex].
From the expansion path, we can draw the total cost curve. We have three points already, X, Y, and Z. Point X describes a quantity of ten million tablets and a total cost of [latex]C_1[/latex]. Point Y describes a quantity of twenty million tablets and a total cost of [latex]C_2[/latex]. Point Z describes a quantity of thirty million tablets and a total cost of [latex]C_3[/latex]. These three cost-quantity pairs are three points on the long-run total cost curve illustrated in figure 8.5.
Remember from chapter 7 that the total cost is the sum of the input costs, [latex]LRTC = wL+rK[/latex]. As we expand output, we must use more inputs, and the increase in labor and capital results in increasing overall cost of production.
A firm’s long-run average cost (LRAC) is the cost per unit of output. In other words, it is the total cost, LRTC, divided by output, [latex]Q[/latex]:
[latex]LRAC(Q)=\frac{LRTC(Q)}{Q}[/latex]
A firm’s long-run marginal cost (LRMC) is the increase in total cost from an increase in an additional unit of output:
[latex]LRMC(Q)=\frac{\Delta LRTC(Q)}{\Delta Q}[/latex]
where [latex]\Delta LRTC(Q)[/latex] is the change in total cost and [latex]\Delta Q[/latex] is the change in output. This is the same thing as the slope of the total cost curve, [latex]LRTC(Q)[/latex].
Figure 8.6 illustrates the relationship between the total cost curve (panel a) and the average and marginal cost curves (panel b).
To see how long-run total and average costs are related, take point A on the total cost curve in figure 8.6. At this point, we can derive the average cost by dividing the vertical distance, which gives us the total cost, by the horizontal distance, which gives us quantity. This is the same thing as the slope of the ray from the origin that connects to point A: it is the “rise” over the “run.” So in panel b, we have the same quantity on the horizontal axis but the slope of the ray connecting to point A, or the average cost, on the vertical axis. Point A is, therefore, a point on the average cost curve. Note that as we move out along the total cost curve, the ray from the origin to the total cost curve becomes less and less steep until point B, after which the slope gets steeper. Thus point B is the point of minimum average cost, as illustrated in panel b.
To understand the relationship between long-run total cost and marginal cost, let’s go back to point A in panel a. The marginal cost is the same as the slope of the total cost curve, and we can illustrate the slope by using a tangent line: a straight line that passes through point A and has the same slope as the curve at that point. This slope gives us the marginal cost. Note that this slope is not as steep as the ray from the origin that defined average cost at this point. Therefore, in panel b, the marginal cost is lower than the average. We can also observe that as we move along the total cost curve, the slope continues to decrease until point C, after which the slope begins to increase. Thus point C is the minimum marginal cost, as illustrated on the marginal cost curve in panel b.
Finally, note that at point B on the total cost curve, the slope of the ray from the origin and the slope of the total cost curve are identical. At this point, the marginal and the average costs are the same, as seen by the intersection of the two curves in panel b.
This relationship between average and marginal costs is not a coincidence; it is always true. When average cost is above marginal cost, average cost must be decreasing. When average cost is lower than marginal cost, average cost must be increasing. And when average and marginal costs are equal, average cost is not changing. This relationship is described in table 8.2 and illustrated in figure 8.7.
| Table 8.2 The relationship between long-run average and marginal costs | |
|---|---|
| Relationship between AC and MC | Resulting change in AC |
| [latex]AC(Q) \lt MC(Q)[/latex] | [latex]AC(Q)[/latex] increasing |
| [latex]AC(Q) \gt MC(Q)[/latex] | [latex]AC(Q)[/latex] decreasing |
| [latex]AC(Q)=MC(Q)[/latex] | [latex]AC(Q)[/latex] constant |
On the left half of figure 8.7, the average cost is above the marginal cost, and thus the average cost is falling. In the right half of figure 8.7, the average cost is below the marginal cost, and thus the average cost is rising. At the intersection of the two curves, the average cost is at its minimum, and the slope of the average cost curve is zero.
Economies and Diseconomies of Scale
An important economic concept associated with the long-run average cost curve is economies of scale. Economies of scale occur when the average cost of production falls as output increases. Similarly, diseconomies of scale occur when the average cost of production rises as output increases. In a typical long-run average cost curve, there are sections of both economies of scale and diseconomies of scale. There is also a point or region of minimum efficient scale where average cost is at its minimum. This is the point where economies of scale are used up and no longer benefit the firm. Figure 8.8 illustrates these points.
8.3 Short-Run versus Long-Run Costs: The Advantage of Flexibility
Learning Objective 8.3: Explain why long-run costs are always as low as or lower than short-run costs and how more flexibility in choosing inputs is always better than less.
Short-run average costs are constrained by the presence of a fixed input. So in the long run, we can always do at least as well as, and often better than, what we do in the short run with respect to cost. We can see this is true by comparing the long-run and short-run average cost curves.
The long-run average cost curve is a type of lower boundary of the short-run cost curves. This can be understood most easily by thinking of a series of short-run average total cost curves, each one for a different level of the fixed input, capital, as shown in figure 8.9.
Since capital is variable in the long run, the long-run average cost is essentially the same as picking among the short-run average total cost curves and combining the capital with the optimal level of labor, or in other words, the minimum ATC.
The long-run average cost curve illustrates the benefit of flexibility: by being able to choose both inputs, the firm can ensure that the efficient mix of the inputs is being used at all times, which keeps costs at their minimum points for all output levels. This flexibility means that we can expect that in the long run, the average cost of production is at least as low as, and generally lower than, what it is in the short run.
8.4 Multiproduct Firms, Learning Curves, and Learning by Doing
Learning Objective 8.4: Explain how making more than one product, learning over time, and learning by producing can lower costs.
A number of other factors matter in a firm’s ability to lower costs. In this section, we look at two of them.
Multiproduct Firms
Often, a firm will make more than one product. This raises the interesting question, When is it better for the same firm to make multiple products than for multiple firms to each make one product? One answer lies in the concept of economies of scope: an economy of scope exists when the average cost of one product falls as the production of another product increases.
Take, for example, a firm that makes large LCD televisions. One expensive component of these displays is the flat glass panels needed for the screen. To make these large screens, very large pieces of glass are manufactured and then cut into individual rectangular pieces for the televisions. Often there are smaller glass pieces left over. Rather than discard these pieces, the same company can make smaller LCD displays for computers, cars, appliances, and so on. Since a lot of the other materials, technical know-how, skilled labor, and the like can be shared across the two types of products, the average cost of both declines when the production of smaller LCD displays for computers is increased.
More formally, we can think of a multiproduct firm as having a cost function that depends on the output of two goods: [latex]Q_1[/latex] and [latex]Q_2[/latex]. Such a cost function can be expressed as [latex]C(Q_1,Q+2)[/latex]. We say the economies of scope are present if
[latex]C(Q_1,Q_2) \lt C(Q_1,0)+C(0,Q_2)[/latex].
This equation makes intuitive sense. The left-hand side of the inequality is the cost of a single firm that produced positive quantities of both goods. The right-hand side is the total cost of producing only [latex]Q_1[/latex] added to the total cost of producing only [latex]Q_2[/latex]. If it is cheaper to produce the two together, then the inequality holds.
Learning Curves
Sometimes firms get better at making things over time, as they gain experience. Economists call this learning by doing. Learning by doing means that as the cumulative output—the total output ever produced—of the firm increases, the average cost falls.
Learning by doing can take different forms:
- Over time, workers become more efficient at specific tasks they perform repeatedly.
- Managers can observe production and adjust task assignments and other aspects of the production process.
- Engineers can optimize product and plant design to increase efficiency.
- Firms can get better at handling inputs, materials, and inventories.
These and other instances of learning by doing often lower firms’ average costs and make them more efficient over time.
The idea of learning by doing can be graphed as a learning curve (figure 8.10) where average cost is plotted as a function of either time or cumulative output. The learning curve is different from the typical average cost curve, which represents the total cost divided by current output.
This temporal view of average costs makes firms’ decisions about operating and investing in the business more complicated. If a firm that is considering shutting down in the face of negative economic profits expects that it will be able to produce more efficiently in the future, it might be willing to accept near-term losses in the expectation of future profits.
The learning curve is potentially important in the policy question. If there is substantial learning involved in the production of a streetcar, then the domestic manufacturer of streetcars might see its production costs decrease significantly as they produce more and more streetcars. So although the short-run costs of production might suggest that domestic promotion is a bad idea, if there is good reason to believe that in the long run, average costs will decrease significantly, a reasonable case could be made for such promotion.
8.5 Policy Example
Should the Federal Government Promote Domestic Production of Streetcars?
Learning Objective 8.5: Use a cost analysis to explain why building streetcars domestically in the United States is or is not a good policy.
To understand the business of building streetcars, we must first think about the cost structure. Streetcars are large, heavy, and loaded with specific and sophisticated technology, such as electric propulsion engines, car electronics and controls, and passenger controls. Their manufacture takes a factory of considerable size, and yet they are produced in small quantities. This suggests a few things about their costs:
- There are very large fixed costs because of the machinery and the plant required for constructing these cars. Because of this, the minimum efficient scale is probably far beyond any one manufacturer’s current scale. What this means is that the more streetcars a manufacturer produces, the lower the cost per car.
- Because of the complexity, there are likely to be large cost savings over time as a result of learning by doing.
- The complexity of the streetcar itself suggests that the quality of the product from new firms might suffer because they have not had the experience that longtime suppliers have had.
These observations suggest that current suppliers of streetcars, like Siemens, have considerable cost advantages over new firms because of their current production level, which allows them to take advantage of economies of scale, and because they are much farther along the learning curve (see figures 8.10 and 8.12). Any new firm likely would take a very long time to reach the current manufacturer’s scale efficiencies and cost efficiencies from learning by doing. However, if the demand for streetcars was expected to grow and be sustained for a long period of time, a reasonable case could be made that the domestic industry could mature into a reliable and cost-efficient supplier of streetcars to the United States and even the international market.
Unfortunately, the projections of the level of demand for streetcars appear to have been far too optimistic. It seems unlikely that the domestic streetcar industry will have a chance to grow and learn, so we may never know if it would have become cost competitive over time.
Exploring the Policy Question
- Because of their size and weight, shipping streetcars internationally is costly. How would you include transportation costs in your analysis of the policy question?
- If the market had not dried up, do you think United Streetcar would have succeeded in the long run? Why or why not? Use economic reasoning in your answer.
REVIEW: TOPICS AND RELATED LEARNING OUTCOMES
8.1 Short-Run Cost Curves
Learning Objective 8.1: Derive the seven short-run cost curves from the total cost function.
8.2 Long-Run Cost Curves
Learning Objective 8.2: Derive the three long-run cost curves from the total cost function.
8.3 Short-Run versus Long-Run Costs: The Advantage of Flexibility
Learning Objective 8.3: Explain why long-run costs are always as low as or lower than short-run costs and how more flexibility in choosing inputs is always better than less.
8.4 Multiproduct Firms, Learning Curves, and Learning by Doing
Learning Objective 8.4: Explain how making more than one product, learning over time, and learning by producing can lower costs.
8.5 Policy Example
Should the Federal Government Promote Domestic Production of Streetcars?
Learning Objective 8.5: Use a cost analysis to explain why building streetcars domestically in the United States is or is not a good policy.
LEARN: KEY TOPICS
Terms
Fixed cost
The cost of production that does not vary with output level. The fixed cost is the cost of the fixed inputs in production, such as the cost of a machine (capital) that costs the same to operate no matter how much production is happening, i.e., a conveyor belt in a factory that moves a streetcar chassis through various stages of an assembly line. The belt is either on or off, but the cost of running it does not change depending on how many streetcars it carries at any point in time.
Variable cost
The cost of production that varies with output level. This is the cost of the variable inputs in production—i.e., the cost of the workers that assemble the electronic devices along a conveyor belt. The number of workers might depend on how many devices the factory is trying to produce in a day. If its production target increases, it uses more labor, thus the hourly wages it pays for these workers are a variable cost. Variable cost generally increases with the amount of output produced.
Total cost
The sum of fixed and variable costs of production.
Average fixed cost
The fixed cost per unit of output.
Average variable cost
The total cost per unit of output. This is the same as the sum of the average fixed cost and the average variable cost.
Average total cost
The total cost per unit of output. This is the same as the sum of the average fixed cost and the average variable cost.
Marginal cost
The additional cost incurred from the production of one more unit of output.
Long-run total cost
In the long-run, all costs are variable. This represents the total cost of all previously fixed and variable inputs.
Long-run average cost
The cost per unit of output. In other words, it is the total cost, LRTC, divided by output, [latex]Q[/latex].
Long-run marginal cost
The increase in total cost from an increase in an additional unit of output.
Expansion path
A curve that shows the cost-minimizing amount of each input for every level of output.
Economies of scale
When the average cost of production falls as output increases,
Diseconomies of scale
When the average cost of production rises as output increases.
Minimum efficient scale
The point on a cost curve where average cost is at its minimum. This is the point where economies of scale are used up and no longer benefit the firm.
Economies of scope
When the average cost of one product falls as the production of another product increases.
Learning by doing
As the cumulative output—the total output ever produced—of the firm increases, the average cost falls.
Learning curve
The graph of a firm’s process of learning by doing. Differs from the typical average cost curve; this is plotted as a function of time or cumulative output.
Graphs
Three short-run cost curves: fixed, variable, and total costs

The total product of labor curve

Marginal cost, average fixed cost, average variable cost, and average total cost

Expansion path
The long-run total cost curve
Deriving long-run average and marginal costs curves from the long-run total cost curve
Relationship between the long-run average and marginal cost curves
The long-run average cost curve as the lower boundary of short-run average cost curves
The learning curve
Equations
Short Run Cost Equations
Fixed Cost
Lacks an exact equation: the fixed cost in the context of short-run curves is the cost even when the output is at zero.
Variable cost
Variable cost varies with output level. Variable costs generally increase with the amount of output produced.
Total cost
The sum of fixed and variable costs of production.
[latex]C = FC + VC[/latex]
Average fixed cost
The fixed cost per unit of output.
[latex]AFC = FC/Q[/latex]
Average variable cost
The variable cost per unit of output.
[latex]AVC = VC/Q[/latex]
Average total cost
The total cost per unit of output. The sum of the average fixed cost and average variable cost
[latex]AC = AC/Q = AFC + AVC[/latex]
Marginal cost
The additional cost incurred from the production of one more unit of output.
[latex]MC=\frac{\Delta C}{\Delta Q}[/latex]
Because the only part of total cost that increases with an additional unit of output is the variable cost, we can re-write the marginal cost as
[latex]MC=\frac{\Delta VC}{\Delta Q}[/latex]
Long-run Cost Equations
Long-run cost minimization problem, review.
Long-run cost minimization problem
The slope of the isoquant is the MRTS, and the slope of the is
[latex]-w/r[/latex]
So the solution to the long-run cost minimization problem is
[latex]MRTS=-\frac{w}{r}[/latex]
or
[latex]\frac{MP_L}{w}=\frac{MP_K}{r}[/latex]
This formula has many different calculus derived conclusions that can be reviewed in chapter 7.
Long-run Total Cost
The sum of the all input costs
[latex]LTRC=wL+rK[/latex]
Long-run average cost (LRAC)
The cost per unit of output. Because there is no fixedcost in the Long-run, it is the total cost [latex]LRTC[/latex], divdied by output [latex]Q[/latex].
[latex]LRAC(Q)=\frac{LRTC(Q)}{Q}[/latex]
Long-run marginal cost
The increase in total cost from an increase in an additional unit of output.
[latex]LRMC(Q)=\frac{\Delta LRTC(Q)}{\Delta Q}[/latex]
Media Attributions
- fig8.1.1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- fig8.1.2 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- fig8.1.3 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 821Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 822Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 823Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 824Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 825Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 831Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 841Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 851Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- 852Artboard-1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license

