2 Utility

The Policy Question
Is a tax credit on hybrid car purchases the government’s best choice to reduce fuel consumption and carbon emissions?
US residents and the government are concerned about the dependence on imported foreign oil and the release of carbon into the atmosphere. In 2005, Congress passed a law to provide consumers with tax credits toward the purchase of electric and hybrid cars.
This tax credit may seem like a good policy choice, but it is costly because it directly lowers the amount of revenue the US government collects. Are there more effective approaches to reducing dependency on fossil fuels and carbon emissions? How do we decide which policy is best? To answer this question, policymakers need to predict with some accuracy how consumers will respond to this tax policy before these policymakers spend millions of federal dollars.
We can apply the concept of utility to this policy question. In this chapter, we will study utility and utility functions. We will then be able to use an appropriate utility function to derive indifference curves that describe our policy question.
Exploring the Policy Question
- Suppose that the tax credit to subsidize hybrid car purchases is wildly successful and doubles the average fuel economy of all cars on US roads—a result that is clearly not realistic but useful for our subsequent discussions. What do you think would happen to the fuel consumption of all US motorists? Should the government expect fuel consumption and carbon emissions from cars to decrease by half in response? Why or why not?
LEARNING OBJECTIVES
2.1 Utility Functions
Learning Objective 2.1: Describe a utility function.
2.2 Utility Functions and Typical Preferences
Learning Objective 2.2: Identify utility functions based on the typical preferences they represent.
2.3 Relating Utility Functions and Indifference Curve Maps
Learning Objective 2.3: Explain how to derive an indifference curve from a utility function.
2.4 Finding Marginal Utility and Marginal Rate of Substitution
Learning Objective 2.4: Derive marginal utility and MRS for typical utility functions.
2.5 Policy Example
Is a Tax Credit on Hybrid Car Purchases the Government’s Best Choice?
Learning Objective 2.5: The Hybrid Tax Credit and customer utility
2.1 Utility Functions
Learning Objective 2.1: Describe a utility function.
Our preferences allow us to make comparisons between different consumption bundles and choose the preferred bundles. We could, for example, determine the rank ordering of a whole set of bundles based on our preferences. A utility function is a mathematical function that ranks bundles of consumption goods by assigning a number to each, where larger numbers indicate preferred bundles. Utility functions have the properties we identified in chapter 1 regarding preferences. That is, they are able to order bundles, they are complete and transitive, more is preferred to less, and in relevant cases, mixed bundles are better.
The number that the utility function assigns to a specific bundle is known as utility, the satisfaction a consumer gets from a specific bundle. The utility number for each bundle does not mean anything in absolute terms; there is no uniform scale against which we measure satisfaction. Its only purpose is in relative terms: we can use utility to determine which bundles are preferred to others.
If the utility from bundle [latex]A[/latex] is higher than the utility from bundle [latex]B[/latex], it is equivalent to saying that a consumer prefers bundle [latex]A[/latex] to bundle [latex]B[/latex]. Utility functions, therefore, rank consumer preferences by assigning a number to each bundle. We can use a utility function to draw the indifference curve maps described in chapter 1. Since all bundles on the same indifference curve provide the same satisfaction and therefore none is preferred, each bundle has the same utility. We can therefore draw an indifference curve by determining all the bundles that return the same number from the utility function.
Economists say that utility functions are ordinal rather than cardinal. Ordinal means that utility functions only rank bundles—they only indicate which one is better, not how much better it is than another bundle. Suppose, for example, that one utility function indicates that bundle[latex]A[/latex] returns ten utils and bundle[latex]B[/latex]twenty utils. We do not say that bundle [latex]B[/latex] is twice as good, or ten utils better, only that the consumer prefers bundle [latex]B[/latex]. For example, suppose a friend entered a race and told you she came in third. This information is ordinal: You know she was faster than the fourth-place finisher and slower than the second-place finisher. You only know the order in which runners finished. The individual times are cardinal: if the first-place finisher ran the race in exactly one hour and your friend finished in one hour and six minutes, you know your friend was exactly 10 percent slower than the fastest runner. Because utility functions are ordinal, many different utility functions can represent the same preferences. This is true as long as the ordering is preserved.
Take, for example, the utility function [latex]U[/latex] that describes preferences over bundles of goods [latex]A[/latex] and [latex]B[/latex]: [latex]U(A,B)[/latex]. We can apply any positive monotonic transformation to this function (which means, essentially, that we do not change the ordering), and the new function we have created will represent the same preferences. For example, we could multiply a positive constant, [latex]\alpha[/latex], or add a positive or a negative constant, [latex]\beta[/latex]. So [latex]\alpha U(A,B)+ \beta[/latex] represents exactly the same preferences as [latex]U(A,B)[/latex] because it will order the bundles in exactly the same way. This fact is quite useful because sometimes applying a positive monotonic transformation of a utility function makes it easier to solve problems.
2.2 Utility Functions and Typical Preferences
Learning Objective 2.2: Identify utility functions based on the typical preferences they represent.
Consider bundles of apples, [latex]A[/latex], and bananas, [latex]B[/latex]. A utility function that describes Isaac’s preferences for bundles of apples and bananas is the function [latex]U(A,B)[/latex]. But what are Isaac’s particular preferences for bundles of apples and bananas? Suppose that Isaac has fairly standard preferences for apples and bananas that lead to our typical indifference curves: he prefers more to less, and he likes variety. A utility function that represents these preferences might be
[latex]U(A,B) = AB[/latex]
If apples and bananas are perfect complements in Isaac’s preferences, the utility function would look something like this:
[latex]U(A,B) = MIN[A,B][/latex]
where the [latex]MIN[/latex] function simply assigns the smaller of the two numbers as the function’s value.
If apples and bananas are perfect substitutes, the utility function is an additive and would look something like this:
[latex]U(A,B) = A + B[/latex]
Cobb-Douglas utility functions are commonly used in economics for two reasons:
- They represent standard preferences, such as more is better and preference for variety.
- They are very flexible and can be adjusted to fit real-world data very easily.
Cobb-Douglas utility functions have this form:
[latex]U(A,B) = A^\alpha B^\beta[/latex]
Because positive monotonic transformations represent the same preferences, one such transformation can be used to set [latex]\alpha + \beta = 1[/latex], which later we will see is a convenient condition that simplifies some math in the consumer choice problem.
Another way to transform the utility function in a useful way is to take the natural log of the function, which creates a new function that looks like this:
[latex]U(A,B) = \alpha ln(A) + \beta ln(B)[/latex]
To derive this equation, simply apply the rules of natural logs. It is important to keep in mind the level of abstraction here. We typically cannot make specific utility functions that precisely describe individual preferences. Probably none of us could describe our own preferences with a single equation. But as long as consumers in general have preferences that follow our basic assumptions, we can do a pretty good job finding utility functions that match real-world consumption data. We will see evidence of this later in the course.
| Preferences | Utility function | Type of utility function |
|---|---|---|
| Love of variety or “well behaved” | [latex]U(A,B) = AB[/latex] | Cobb-Douglas |
| Love of variety or “well behaved” | [latex]U(A,B) = A^\alpha B^\beta[/latex] | Cobb-Douglas |
| Love of variety or “well behaved” | [latex]U(A,B) = \alpha ln(A) + \beta ln(B)[/latex] | Natural log Cobb-Douglas |
| Perfect complements | [latex]U(A,B) = MIN[A,B][/latex] | Min function |
| Perfect substitutes | [latex]U(A,B) = A + B[/latex] | Additive |
2.3 Relating Utility Functions and Indifference Curve Maps
Learning Objective 2.3: Explain how to derive an indifference curve from a utility function.
Indifference curves and utility functions are directly related. In fact, since indifference curves represent preferences graphically and utility functions represent preferences mathematically, it follows that indifference curves can be derived from utility functions.
In univariate functions, the dependent variable is plotted on the vertical axis, and the independent variable is plotted on the horizontal axis, like the graph of [latex]y=f(x)[/latex]. In contrast, graphs of bivariate functions are three-dimensional, like [latex]U=U(A,B)[/latex]. Figure 2.1 shows a graph of [latex]U=A^\frac{1}{2}B^\frac{1}{2}[/latex]. Three-dimensional graphs are useful for understanding how utility increases with the increased consumption of both A and B.
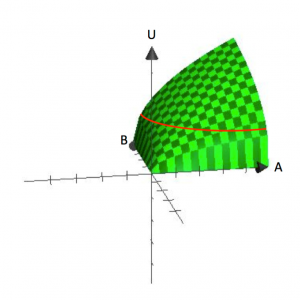
Figure 2.1 clearly shows the assumption that consumers have a preference for variety. Each bundle, which contains a specific amount of [latex]A[/latex] and [latex]B[/latex], represents a point on the surface. The vertical height of the surface represents the level of utility. By increasing both [latex]A[/latex] and [latex]B[/latex], a consumer can reach higher points on the surface.
So where do indifference curves come from? Recall that an indifference curve is a collection of all bundles that a consumer is indifferent about with respect to which one to consume. Mathematically, this is equivalent to saying all bundles, when put into the utility function, return the same functional value. So if we set a value for utility, [latex]Ū[/latex], and find all the bundles of [latex]A[/latex] and [latex]B[/latex] that generate that value, we will define an indifference curve. Notice that this is equivalent to finding all the bundles that get the consumer to the same height on the three-dimensional surface in figure 2.1.
Indifference curves are a representation of elevation (utility level) on a flat surface. In this way, they are analogous to a contour line on a topographical map. By taking the three-dimensional graph back to two-dimensional space—the A, B space—we can show the contour lines / indifference curves that represent different elevations or utility levels. From the graph in figure 2.1, you can already see how this utility function yields indifference curves that are “bowed-in” or concave to the origin.
So indifference curves follow directly from utility functions and are a useful way to represent utility functions in a two-dimensional graph.
2.4 Finding Marginal Utility and Marginal Rate of Substitution
Learning Objective 2.4: Derive marginal utility and MRS for typical utility functions.
Marginal utility [latex](MU)[/latex] is the additional utility a consumer receives from consuming one additional unit of a good. Mathematically, we express this as
[latex]MU_{A}=\frac{\Delta U}{\Delta A}[/latex]
or the change in utility from a change in the amount of [latex]A[/latex] consumed, where Δ represents a change in the value of the item, so
[latex]MU_{A}=\frac{\Delta U}{\Delta A}=\frac{U (A+\Delta A,B)-U(A,B)}{\Delta A}[/latex]
Note that when we are examining the marginal utility of the consumption of [latex]A[/latex], we hold [latex]B[/latex] constant.
Using calculus, the marginal utility is the same as the partial derivative of the utility function with respect to [latex]A[/latex]:
[latex]MU_{A}=\frac{\partial U(A,B)}{\partial A}[/latex]
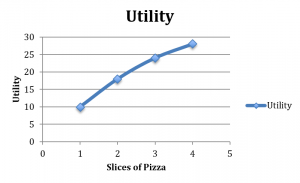
Consider a consumer who sits down to eat a meal of salad and pizza. Suppose that we hold the amount of salad constant—one side salad with a dinner, for example. Now let’s increase the slices of pizza; suppose with one slice, utility is ten; with two, it is eighteen; with three, it is twenty-four; and with four, it is twenty-eight. Let’s plot these numbers on a graph that has utility on the vertical axis and pizza on the horizontal axis (table 2.2 and figure 2.2).
| Total pizza slices consumed | Utility | Marginal utility |
|---|---|---|
| 1 slice | 10 | N/A; no margin |
| 2 slices | 18 | 8 |
| 3 slices | 24 | 6 |
| 4 slices | 28 | 4 |
Media Attributions
- “Fill ‘Er Up” © Derek Bruff is licensed under a CC BY-NC (Attribution NonCommercial) license
- fig2.1-768×768 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 2.4.1 Diminish Marginal Utility © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 2.5.1 Graph of indifference curves for the policy example © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
A mathematical function that ranks bundles of consumption goods by assigning a number to each, where larger numbers indicate preferred bundles.
The satisfaction a consumer gets from a specific bundle.
Ordinal information does not apply a direct value to the comparison. If someone is faster, in an ordinal comparison we wouldn't say she is forty times faster, only that she is faster.
Cardinal information points in a specific direction instead of just in a general order. In a race, the first-place finisher ran the race finished in exactly one hour and your friend finished in one hour and six minutes. The cardinal information allows you to know your friend was exactly 10 percent slower than the fastest runner.
The order the race was completed, therefore, is ordinal, but the times the runners completed the race with is cardinal.
A util is a generic unit of measurement used for bundle comparisons. Because bundle comparisons for utility are ordinal, we have no specific units in which to determine preference. Instead, we assign utils as a way to talk in comparison about preferences.
Ten utils for bundle A and twenty utils for bundle B does not mean bundle B is preferred twice as much, as we've no idea what 10 utils and 20 utils derives from—all we know is that 20 is bigger than 10, and so B is preferred.
The ordering of an ordinal function isn't changed in the process of transforming the equation.
See Section 1.5.1: Perfect Complements.
Goods that consumers want to consume only in fixed proportions, i.e., airpods to an iPhone.
Perfect complement indifference curves have right angles.
See Section 1.5.2: Perfect Substitutes.
A good that makes a consumer just as well off as a fixed amount of another good, i.e., Morton and Diamond Crystal are brands of table salt. For most consumers, a teaspoon of one salt is always just as good as a teaspoon of the other.
The graph for a perfect substitute is a straight-forward linear equation (y=mx+b).
The Cobb-Douglas functional form was first proposed as a production function in a macroeconomic setting, but its mathematical properties are also useful as a utility function describing goods which are neither complements nor substitutes.
A consumer that conforms to the "well-behaved" conditions of consumer preferences, and thus the indifference curve for this consumer's choice problem behaves as expected.
See Section 1.1.
Sometimes presented as more-is-better.
If bundle [latex]A[/latex] represents more of at least one good and no less of any other good than bundle [latex]B[/latex], then [latex]A[/latex] is preferred to [latex]B[/latex].
The idea that customers prefer choices in their consumption. Suppose we are talking about miles driven in a month in comparison to the cost in gas it takes to do such a thing: a customer will rarely want to spend all of their money on gas for miles driven, but also will not be likely to choose simply to not drive at all. Thus, a preference for variety.
A function with one variable.
A function with two variables.
See Chapter 1.
A graph of all the combinations of bundles that a consumer prefers equally. In other words, the consumer would be just as happy consuming any of them.
Wavy, circular lines employed on a two-dimensional topographic map that depict elevation on the ground. The distance between each contour line is set to represent a certain level of elevation with zero being sea level.
See Section 2.4.
The additional utility a customer receives from consuming one additional unit of a good.
[latex]MU_{a}=\frac{\Delta U}{\Delta A}[/latex]
or the change in utility from a change in the amount of A consumed, where [latex]\delta[/latex] represents a change of value in the item.

![Figure 2.1 A 3D graph showing a graph of [latex]U[/latex] equals [latex]A^\frac{1}{2}[/latex] times [latex]B^\frac{1}{2}[/latex] to the half power](https://open.oregonstate.education/app/uploads/sites/203/2023/01/fig2.1b.png)
