Es posible espiar comunicaciones a través de internet en muchos puntos: el hotspot wi-fi al cual estás conectado directamente, tu proveedor de internet, el servidor que aloja las páginas web que visitas, portales nacionales y la vasta selección de enrutadores e interruptores ubicados en medio.

Sin un cifrado, todas estas comunicaciones pueden ser interceptadas por un espía, ya sea un acosador, un pirata informático o una agencia gubernamental. Pero con el fin de cifrar tus comunicaciones, necesitas acordar una clave con tu interlocutor. Si estás visitando un sitio web, ¿cómo intercambias de manera segura una clave con el servidor que aloja el sitio? Para acordar una clave sin reunirse y a través de canales de comunicación inseguros como internet, es necesario un método bipartito (por ejemplo, dos personas, una persona y un servidor, o dos servidores).

Un ejemplo físico: intercambiar un mensaje sin intercambiar una llave

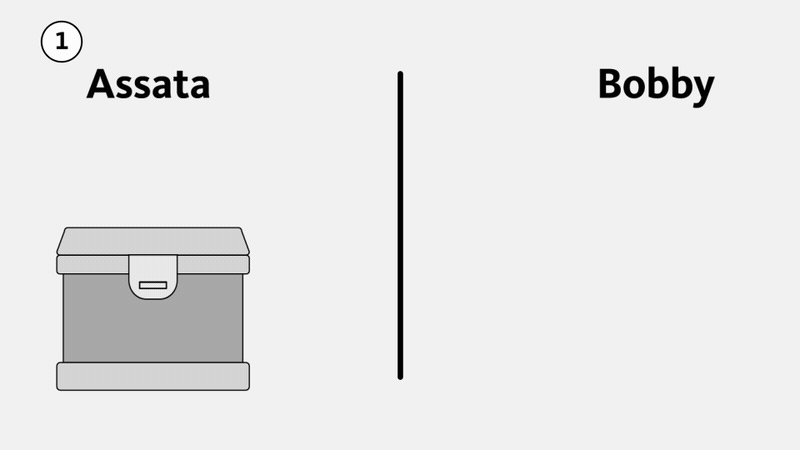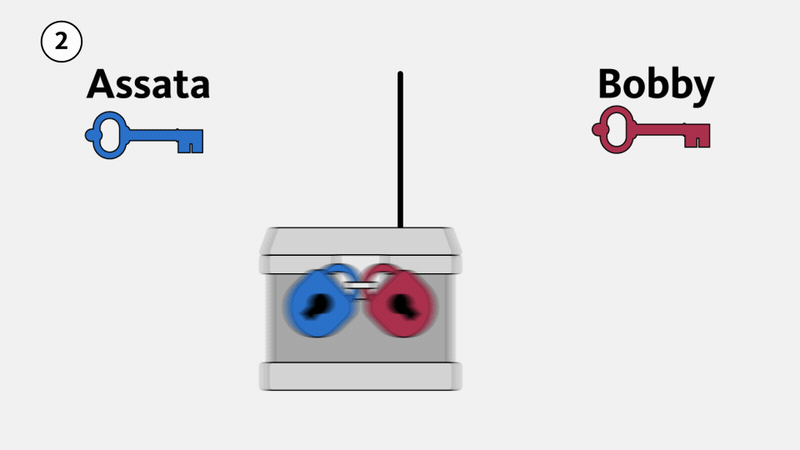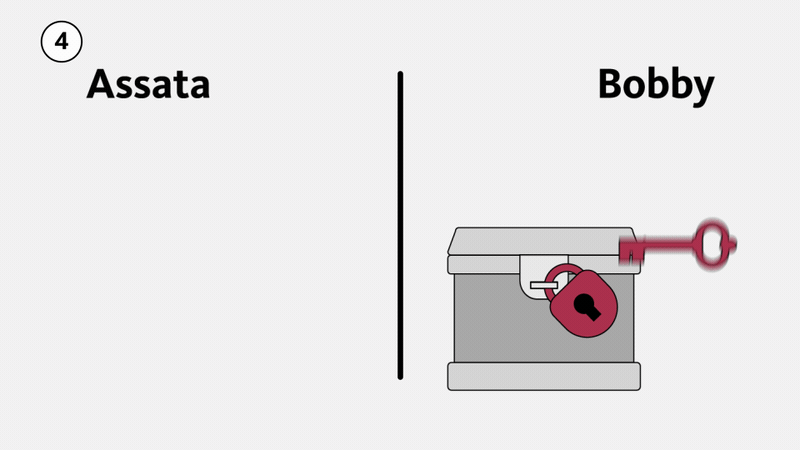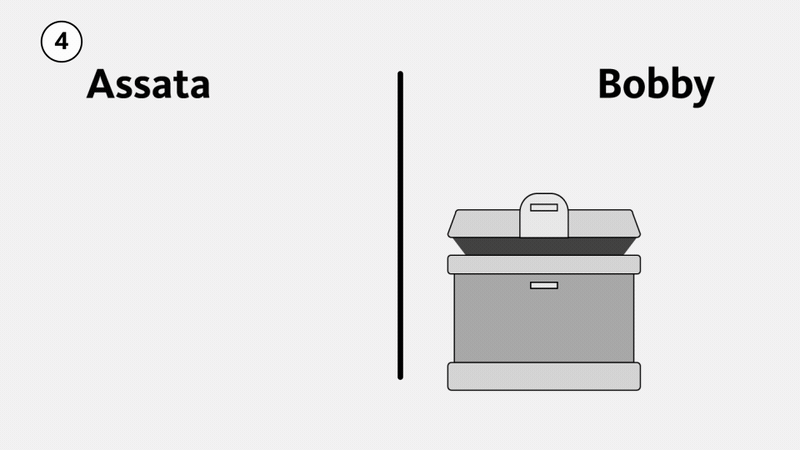
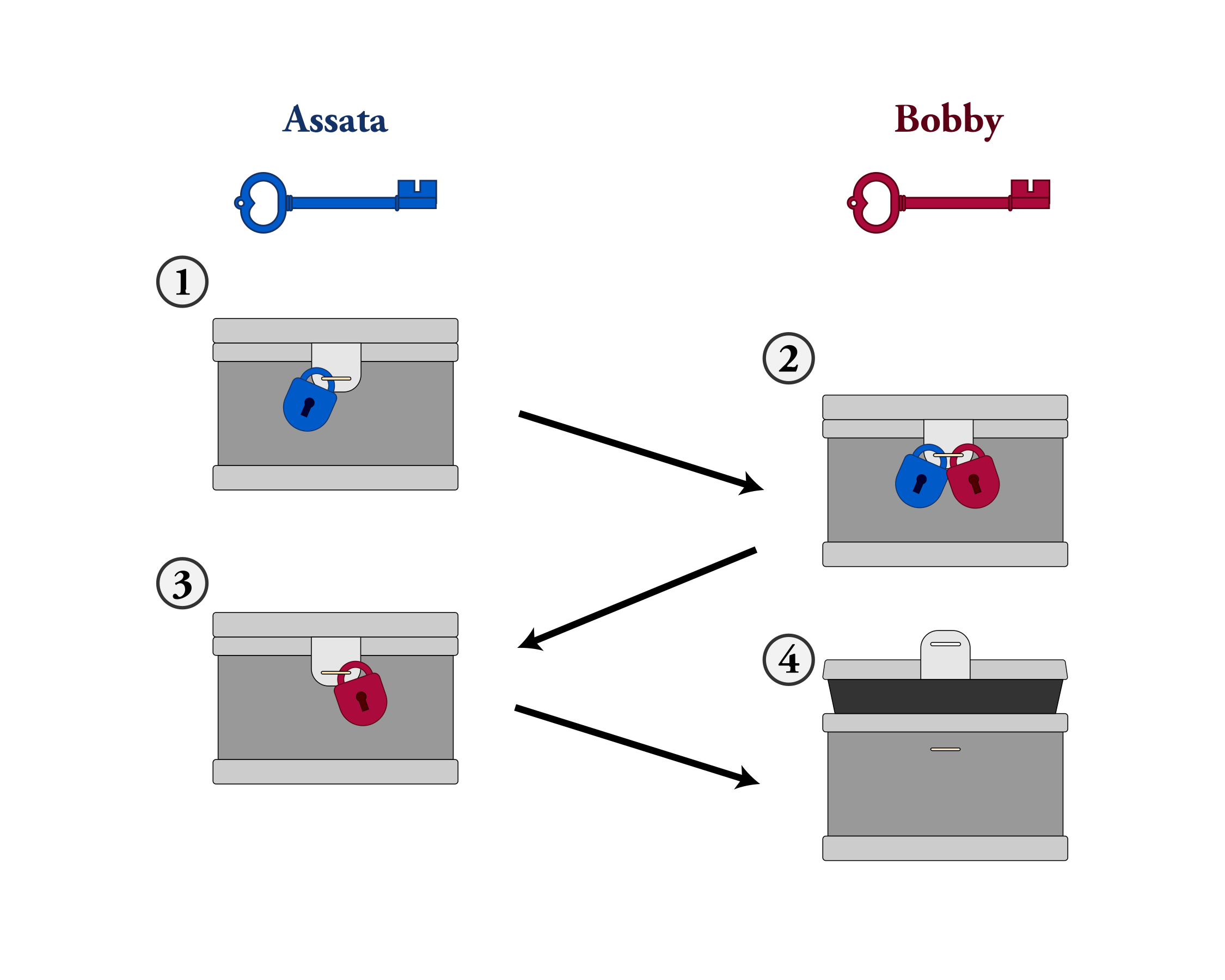
Primero, consideremos el ejemplo físico que se ilustra abajo. Supongamos que Assata quiere enviarle un paquete a Bobby. Lo pone en una caja fuerte con una hebilla en la que caben diferentes candados (1) y pone un candado en la caja, del cual Bobby no tiene la llave. Assata le envía la caja a Bobby, quien no puede abrirla (y tampoco puede abrirla otra persona mientras está en tránsito). Luego, Bobby le pone su propio candado a la caja (2), un candado del cual Assata no tiene la llave, y se la reenvía. Cuando Assata recibe la caja, le quita su propio candado y envía la caja de vuelta a Bobby (3). Ahora Bobby puede abrir la caja porque solo está asegurada con su candado (4). La caja no puede abrirse en tránsito, pues un espía tendría que romper el candado de Assata, el de Bobby, o ambos.

Esto ilustra que es posible enviar algo de forma segura sin reunirse antes para intercambiar (acordar) una clave. Sin embargo, no vamos a comenzar a enviar cajas fuertes por correo con el fin de intercambiar claves criptográficas. Lo que se necesita es una versión matemática de esto que se pueda usar con comunicaciones digitales.

Un ejemplo matemático: intercambiar un mensaje sin intercambiar una clave

Veamos cómo hacer esto sin cajas fuertes y candados. Supongamos que hay un protocolo de cifrado con el cual se puede cifrar cualquier texto (como se espera siempre), que el protocolo se puede aplicar en múltiples ocasiones para tener capas de cifrado (como también siempre se espera) y que dichas capas se pueden cifrar y descifrar en cualquier orden y terminar con el mismo resultado. Una operación matemática que satisfaga esta última propiedad se conoce como conmutativa. (Todos los protocolos descritos en el capítulo ¿Qué es el cifrado? son conmutativos.) Veamos esto con un ejemplo, usando el cifrado Vigenère.

Assata cifra el siguiente mensaje

EN ALGUN MOMENTO HUBO EN ESTE MUNDO BOSQUES QUE NO ERAN DE NADIE

con un cifrado Vigenère y la clave ALDO, para obtener el siguiente texto cifrado:

EY DZGFQ AOXHBTZ KIBZ HB EDWS MFQRO MRGQFHG QFH BO PUON OH BAOLS

Luego, le envía el resultado a Bobby, aunque ¡él no tiene la clave! Bobby, a su vez, cifra este texto ya cifrado con un cifrado Vigenère y el código LEOPOLDO, para obtener el siguiente texto doblemente cifrado:

PC ROUQT OZBVQHK NWMD VQ SOZG XJEGC XUUBJVV EQK PZ TIDB ZK PLSZH

Posteriormente, Bobby le envía el resultado a Assata, quien “descifra” el mensaje con su clave (ALDO) y obtiene el siguiente mensaje (aun cifrado):

PR OAUFQ AZQSCHZ KIMS SC SDWS XYBSC MRGBYSH EFH BZ IFPB OH BLHWT

Assata le envía de nuevo el resultado a Bobby, quien finalmente lo descifra con su propia clave (LEOPOLDO) y obtiene el mensaje que Assata quería enviarle en primer lugar:

EN ALGUN MOMENTO HUBO EN ESTE MUNDO BOSQUES QUE NO ERAN DE NADIE

Se debe observar que en este ejemplo Assata no compartió su clave (ALDO) con nadie, y Bobby tampoco compartió la suya (LEOPOLDO) con nadie. Puesto que el cifrado Vigenère es conmutativo, no importa que el mensaje estuviera cifrado con la clave de Assata, luego con la de Bobby, luego descifrado con la de Assata y finalmente descifrado con la de Bobby. Lo único que importa es que el mensaje fue cifrado y descifrado una vez con cada una de las claves. Cualquier espía vería solamente uno de los tres textos cifrados intermedios.

Un ejemplo físico: acordar un secreto por un canal no seguro

En los sistemas criptográficos modernos, en lugar de enviar el mensaje completo una y otra vez, con diferentes capas de cifrado, se hace un intercambio inicial, parecido a los ejemplos anteriores, para acordar una clave. Podríamos imaginar que Assata, en lugar de enviar el mensaje EN ALGUN MOMENTO HUBO…, envía una clave criptográfica para usar en una comunicación más amplia. Describiremos el fundamento matemático para el intercambio de claves como se usa en casi todas las comunicaciones modernas, conocido como protocolo criptográfico Diffie-Hellman.

Primero, veamos cómo se hace con pinturas y no con matemáticas (se ilustra a continuación). Se asumirá que, si se mezclan dos colores de pintura, no es posible volver a separarlos; específicamente, aunque se supiera cuál fue uno de los colores iniciales, no se podría determinar con cuál color se mezcló para obtener el color resultante.

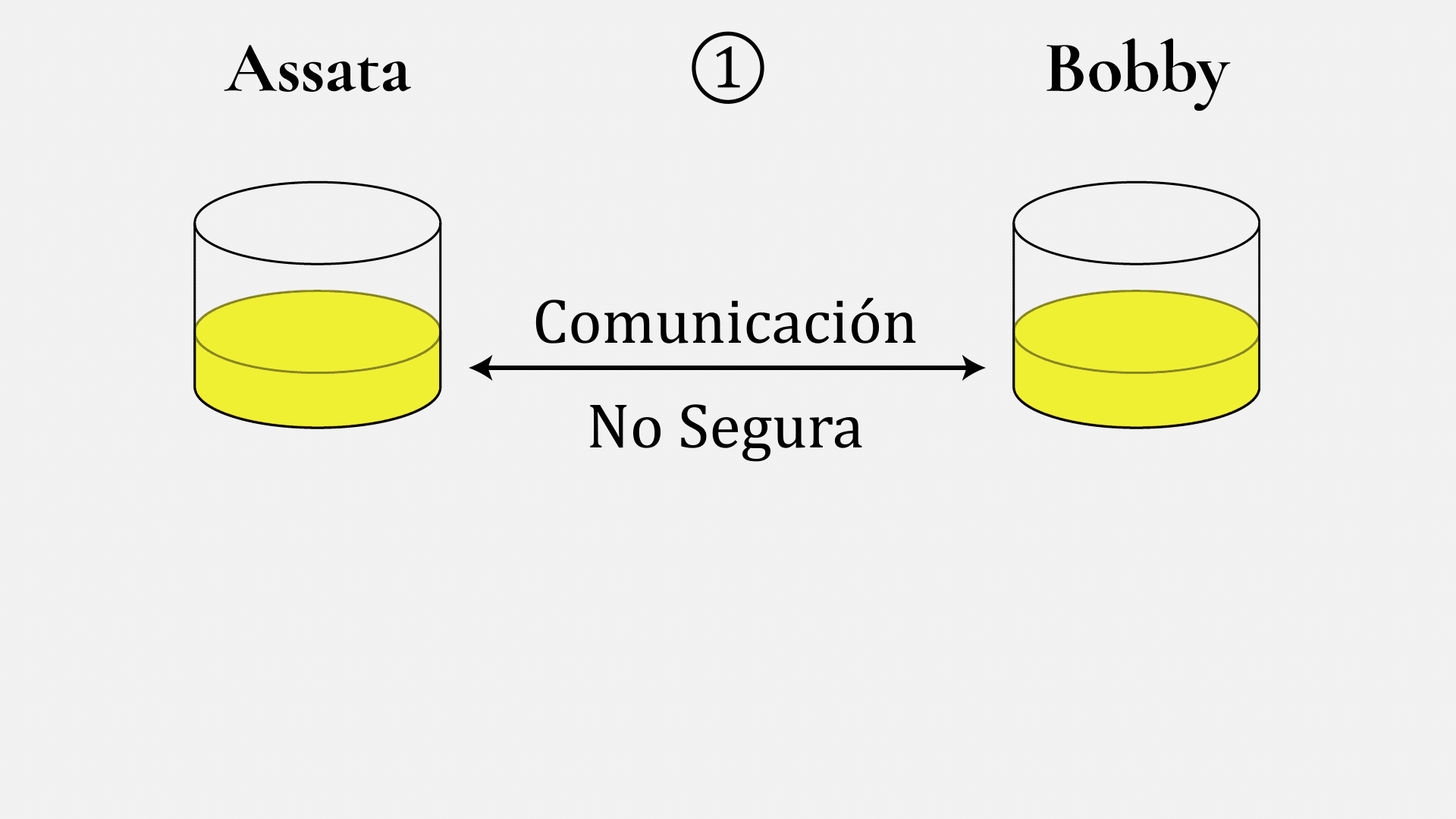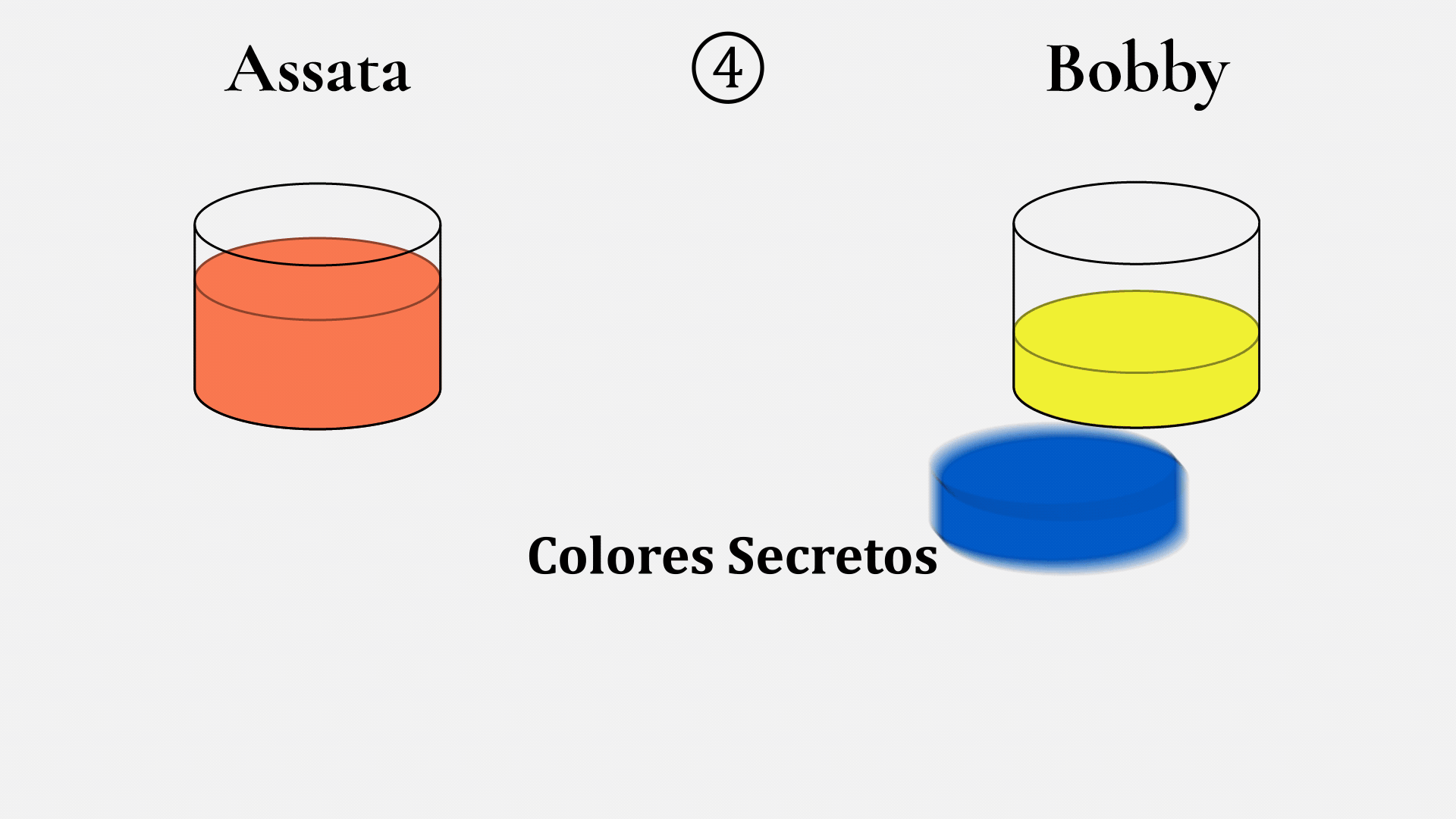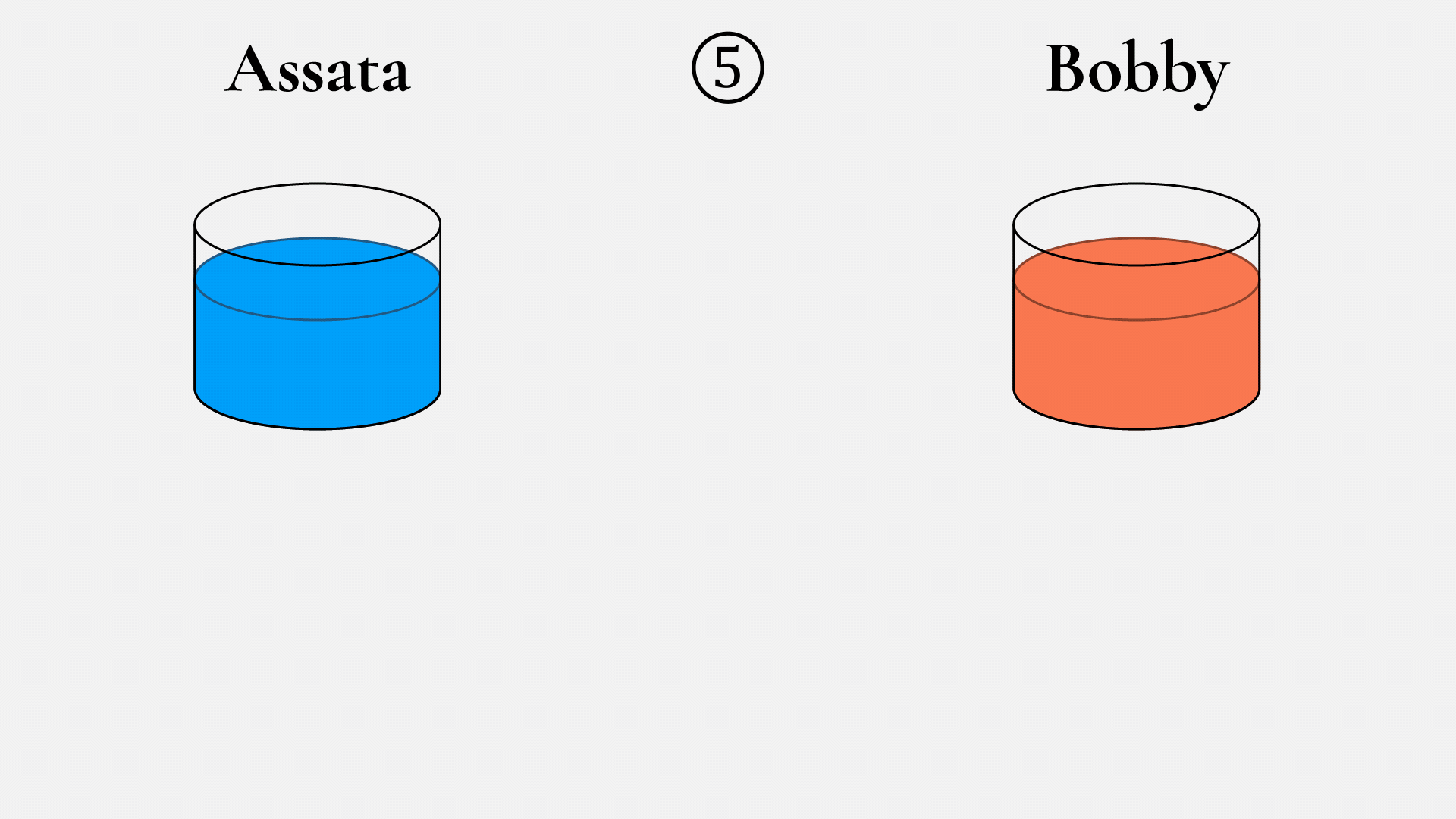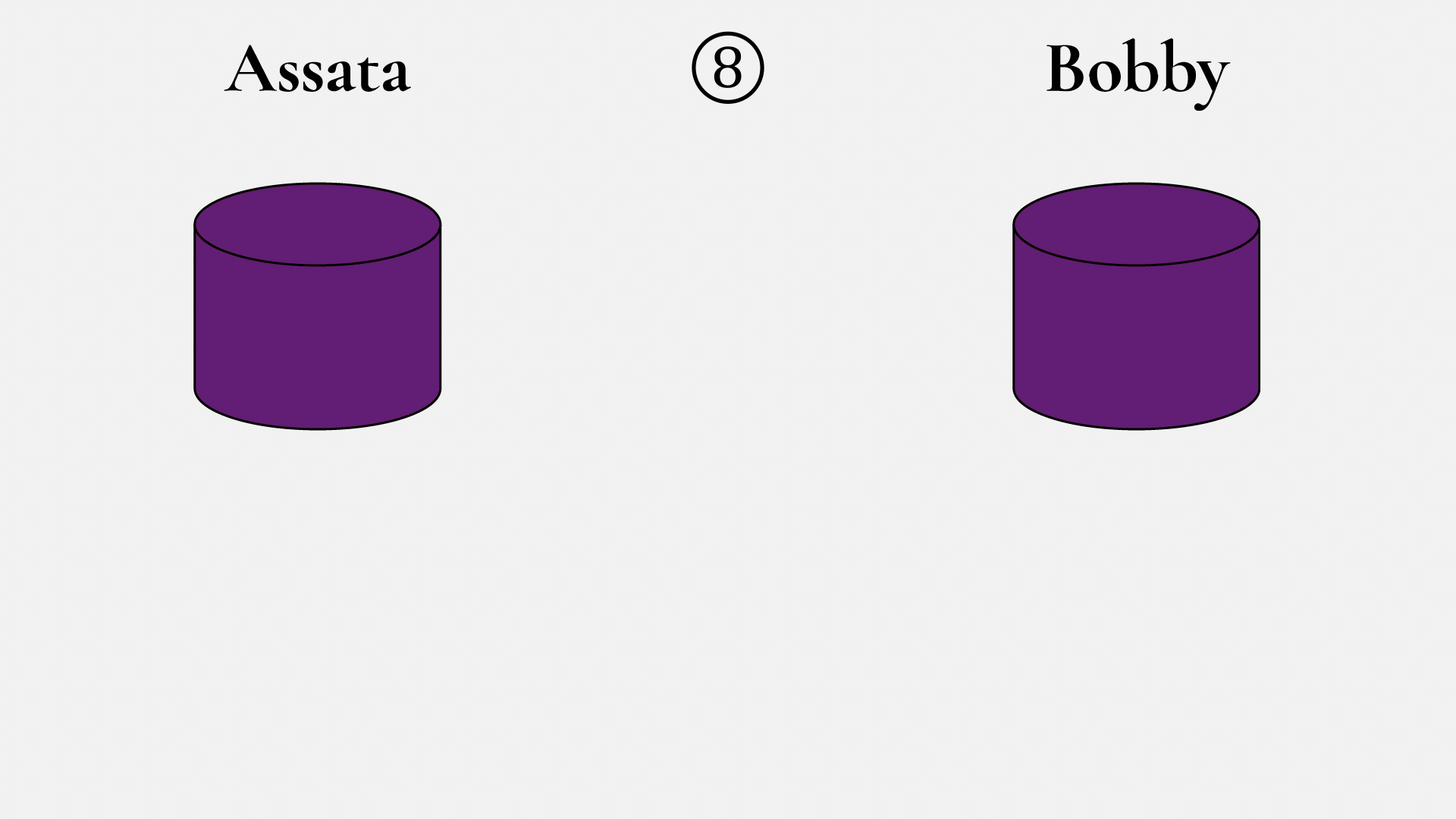
Assata y Bobby comienzan acordando un color de pintura (en este ejemplo, el amarillo) y una cantidad, digamos, 10 mL (1). Esto pueden hacerlo a través de un canal de comunicación no seguro, pero deben asumir que entonces un espía también conocerá el color y la cantidad. Después, Assata elige un color (en este caso, el bermellón) y lo mantiene en secreto (2). Luego, mezcla 10 mL de amarillo con 10 mL de bermellón y obtiene un color anaranjado (3), y lo envía a Bobby a través del canal no seguro, en el entendido de que un espía también lo verá. Bobby hace lo mismo, con su propio color secreto (4).

Ahora, a la muestra de pintura enviada por Bobby (5), Assata le añade 10 mL de su color secreto (6), lo cual resulta en un violeta intenso (7). Bobby hace lo mismo. El desagradable color violeta intenso de Assata se obtiene mezclando 10 mL de cada uno de estos colores: amarillo, su color secreto y el color secreto de Bobby. El color resultante de Bobby se obtiene mezclando 10 mL de amarillo, 10 m de su color secreto y 10 m del color secreto de Assata. ¡Así que Bobby obtiene el mismo desagradable color violeta intenso (8)! ¿Puede el espía crear el color violeta intenso? El espía ve el amarillo (1), la mezcla de amarillo con el color secreto de Assata (3) y la mezcla de amarillo con el color secreto de Bobby (5). Pero para crear ese horrible violeta intenso, el espía tendría que separar las mezclas de colores para obtener los colores secretos de Assata o Bobby, lo cual no puede hacer.

El protocolo criptográfico Diffie-Hellman

Repasemos este mismo proceso matemáticamente. Esto se hace con una operación matemática conmutativa que sea difícil o imposible revertir. Una operación matemática o función difícil o imposible de revertir se conoce como función unidireccional. Representemos nuestra operación matemática con el símbolo ☆; es decir, a ☆ b = c para algunos números a, b y c. Conmutativo significa que a ☆ b = b ☆ a. Por otra parte, que ☆ sea unidireccional significa que si se conoce b y c, no se puede deducir fácilmente qué es a. En la práctica, solo se debería poder descifrar qué es a mediante un ataque de fuerza bruta o casi de fuerza bruta (probar todas y cada una de las posibilidades para a). Pensemos en ☆ como el signo de multiplicación (el cual es conmutativo, pero no unidireccional). Para aquellos con inclinación hacia la matemática, ☆ puede ser una exponenciación modular para implementaciones reales de Diffie-Hellman.

A continuación se ilustra la forma en que Assata y Bobby se ponen de acuerdo sobre un número p, el cual es público (1). Assata elige un número secreto a (2), hace el cálculo p ☆ a (3) y envía el resultado a Bobby. Puesto que ☆ es unidireccional, un espía conocería p y p óa, pero no podría determinar a (con facilidad). Bobby elige un número secreto b (4), hace el cálculo p ☆ b y envía el resultado a Assata (5). Un espía conocería p ☆ b, pero no b. Luego, Assata hace el cálculo (p ☆ b) ☆ a (7) usando el mensaje de Bobby (5) y su propio número secreto (6). Entonces, Bobby hace el cálculo (p ☆ a) ☆ b (8) usando el mensaje de Assata (3) y su propio número secreto (4). Puesto que ☆ es conmutativo, (p ☆ b) ☆ a = (p ☆ a) ☆ b, así que Assata y Bobby ahora han calculado un número común. Puesto que el espía solo conoce p ☆ a, p ☆ b y p, y puesto que ☆ es unidireccional, no cuenta con medios eficientes para calcular el número común que calcularon Assata y Bobby: es un secreto entre Assata y Bobby. Por tanto, Assata y Bobby pueden usar este número compartido como su clave criptográfica.

Usar el protocolo Diffie-Hellman

El protocolo Diffie-Hellman es un método de uso generalizado para acordar una clave criptográfica. Es el fundamento de la mayoría de las formas de comunicación cifrada que encontrarás. Lo que es más notable: es la base del intercambio de claves cuando te conectas con un sitio https. Cuando visitas un sitio, la dirección URL se inicia con http:// o con https://. En el primer caso, ninguna de tus comunicaciones con el servidor del sitio está cifrada; en el segundo sí lo están y la clave que se usa para ello se genera usando el protocolo Diffie-Hellman.

En contexto: Cuando algo bueno sale mal

Recuerda que lo primero que hicieron Assata y Bobby fue ponerse de acuerdo en un número p que formó la base de su intercambio de claves.

Este número es público, pero asumimos que nuestra operación matemática ☆ era unidireccional, así que estaba bien que p fuera del conocimiento público. Sin embargo, alguien con muchos recursos de cómputo (como un Estado-nación adinerado) puede invertir la operación ☆ (para funciones como la exponenciación modular usada como ☆ en el mundo real) en dos fases. La primera fase toma mucho tiempo y debe efectuarse para un valor específico de p. La segunda fase puede hacerse con mucha rapidez (en tiempo real) para el mismo valor de p, suponiendo que la primera fase se ha completado. Esto significa que todos deberían evitar usar el mismo valor de p; deberían usar diferentes valores de p, y cambiarlos con frecuencia.

Sin embargo, en 2015, investigadores demostraron que 18 por ciento del millón de dominios https principales usa el mismo valor de p. Otros dos protocolos de comunicación que dependen del protocolo de intercambio Diffie-Hellman son SSH (Secure Shell) y VPN (Virtual Private Network). Los mismos investigadores demostraron que 26 por ciento de los servidores SSH y 66 por ciento de los VPN usan el mismo valor de p en su intercambio Diffie-Hellman. Esto significa que un adversario con recursos tendría muy poca dificultad para deshacer el cifrado.

Aunque el protocolo Diffie-Hellman es fuerte y confiable, esto pone de relieve que quienes implementan los protocolos necesitan hacerlo con cuidado para asegurarse de que, de hecho, son seguros.