Chapter 2: Sequence Motifs
2.1 Introduction to Motifs
A biological motif, broadly speaking, is a pattern found occurring in a set of biological sequences, such as in DNA or protein sequences. A motif could be an exact sequence, such as [latex]\texttt{TGACGTCA}[/latex], or it could be a degenerate consensus sequence, allowing for ambiguous characters, such as [latex]\texttt{R}[/latex] for [latex]\texttt{A}[/latex] or [latex]\texttt{G}[/latex]. Motifs can also be described by a probabilistic model, such as a position-specific scoring matrix (PSSM) or weight matrix.
2.2 String Matching
Frequently we want to search for an exact string or pattern within a larger sequence. For example, when using a restriction enzyme to cut a larger sequence at sequence-specific sites that match a particular pattern, we would like know where this pattern occurs in the larger sequence. This task can be called string matching. There are numerous algorithms that have been developed to make this task more efficient, such as the Knuth-Morris-Pratt algorithm [9] and the Burrows-Wheeler transform [10]. These approaches are beyond the scope of this course, but definitely worth mentioning. Let’s examine how to utilize the Biopython function [latex]\texttt{nt\_search}[/latex] as part of the [latex]\texttt{SeqUtils}[/latex] module. We can use the function as follows to search for the short pattern [latex]\texttt{ACG}[/latex].
>>> from Bio.Seq import Seq
>>> from Bio import SeqUtils
>>> pattern = Seq("ACG")
>>> sequence = Seq("ATGCGCGACGGCGTGATCAGCTTATAGCCGTACGACTGCTGCAACGTGACTGAT")
>>> results = SeqUtils.nt_search(str(sequence),pattern)
>>> print(results)
['ACG', 7, 31, 43]
You’ll note that the function takes in two arguments. The first is the sequence to search, but it is not a [latex]\texttt{Seq}[/latex] object, but the basic python string. The python function “str()” converts the [latex]\texttt{Seq}[/latex] object into a string. The second argument is the pattern or string that we are searching, but this argument clearly can be the [latex]\texttt{Seq}[/latex] object, which it is in this example.
Typically, we consider the DNA sequence that we are searching as double stranded, hence we want to search the forward strand and its reverse complement. In many cases for bioinformatics, such as searching an entire chromosome, it is easier to reverse complement the pattern rather that the sequence to search. In this example, this looks like
>>> results_rc = SeqUtils.nt_search(str(sequence),pattern.reverse_complement())
>>> print(results_rc)
['CGT', 11, 28, 44]
In this example, we have searched the forward strand of the DNA sequence. Alternatively, a biologist might want to know where the patterns occurs with positions defined along the reverse complement of the sequence we are searching, or the reverse strand if the DNA is double stranded. In the example of the restriction enzyme, positions defined along the reverse complement of the larger sequence are more useful for predicting the length of the resulting fragments after treatment by the restriction enzyme. This is performed as follows.
>>> results_rc = SeqUtils.nt_search(str(sequence.reverse_complement()),pattern)
>>> print(results_rc)
['ACG', 7, 23, 40]
The results are clearly different in terms of the positions, but they represent the same information. Because the larger sequence has a length of [latex]54[/latex]nt, we can see that we can transform between the two sets of position with the following equation:
[latex]\texttt{pos1} = \texttt{len(sequence)} - \texttt{pos2} - \texttt{len(pattern)}[/latex]
(2.1)
Where [latex]\texttt{pos1}[/latex] is the position resulting from searching the reverse complement of the pattern over the forward strand of the sequence, and [latex]\texttt{pos2}[/latex] is the position of searching the pattern over the reverse strand of the sequence.
Exercise 6
Find the number of occurrences and locations of [latex]\texttt{ACTT}[/latex] within the following sequence:
>sequence
AGCGATCTAGCATACTTATACGCGCGCAGCTATCGATCACTTGTGCTAGTAAAGTGCGCGCCGCA
TTAAAGTGCTAGCTAGCTACTTAGCTAGCTAGTCG
2.3 Consensus Sequences
A consensus sequence is a string of either nucleotide or protein characters along with “degenerate characters”, which specify a subset of characters. These degenerate characters can act as “wild cards”, such as [latex]\texttt{N}[/latex], which can refer to any character, and are summarized in Table 2.1 [11]. They can also specify a more specific subset, such as [latex]\texttt{Y}[/latex], which specifies the pyrimidines [latex]\texttt{C}[/latex] and [latex]\texttt{T}[/latex].
| Symbol | Meaning | Mnemonic |
|---|---|---|
| R | A, G | puRine |
| Y | C, T | pYrimidine |
| W | A, T | Weak (weaker basepairs, fewer hydrogen bonds) |
| S | G, C | Strong (stronger basepairs, more hydrogen bonds) |
| K | G or T | Keto (both have a keto group) |
| M | A or C | aMine (both have an amine group) |
| B | C, G, T | not A (B comes after A) |
| D | A, G, T | not C (D comes after C) |
| A | A, C, T | not G (H comes after G) |
| V | A, C, G | not T or U (V comes after T and U) |
| N | A, C, G, T | aNy base |
We can combine the standard nucleotides and IUPAC codes to form a “consensus sequence” describing a motif. For example, “Downstream Promoter Element” (DPE) in Drosophila occurs near position +28 from the TSS of many genes, and has the consensus sequence [latex]\texttt{RGWY}[/latex]V [12].
2.3.1 Searcing Consensus Sequences with Biopython
Biopython can also be used to search for a consensus sequence. The [latex]\texttt{SeqUtils.nt\_search()}[/latex] function is built to recognize patterns that include the wild-card characters presented in Table 2.1. If we are to search for the consensus sequence for the DPE, we would use something like this:
>>> from Bio import SeqUtils
>>> consensus = "RGWYV"
>>> sequence = "CGTAGCTAGCTCAGAGCAGGGACACGTGCTAGCAACAGCGCT"
>>> SeqUtils.nt_search(sequence,consensus)
['[AG]G[AT][CT][ACG]', 19]
As before, the results contain the pattern searched and the positions of the instances, but the wild-chard characters of the pattern are now represented in a more traditional regular expression format, with sets of character within square brackets.
2.4 Motif Finding
Motif finding can be described as the process of discovering patterns within collections of sequences. In many cases, we don’t know what the pattern looks like, and this task is a “needle in a haystack” challenge, that involves sifting through many [latex]K[/latex]-mers that aren’t part of the pattern, but occur frequently.
2.4.1 Sequence Complexity
Before we can start looking for motifs, we’ll need to consider things are frequently occur in biological sequence datasets, in particular DNA sequences. The most frequent [latex]K[/latex]-mer in the human genome is “AAAAAAAA”. Such a sequence can be called a “low complexity” sequence, and along with simple repeats, are commonly occurring sequences that can confound motif finding and sequence alignment. Sequences like “ATATATATAT” are also frequently occurring in virtually any sequence dataset, and would be discovered by a motif search if not filtered out.
The Wooton-Federhen complexity is a score that quantifies the complexity of a sequence [13]. Put simply, the WF complexity quantifies the number of possible sequences that could be generated using the same number of As [latex]n_A[/latex], number of Cs [latex]n_C[/latex], number of Gs [latex]n_G[/latex] and number of Ts [latex]n_T[/latex]. This can be computed from a multinomial coefficient, which finds itself in a log in the equation:
[latex]C_{WF} = \frac{1}{N} \log_D \left( \frac{N!}{n_A! n_C! n_G! n_T!} \right)[/latex]
Note that the [latex]\log()[/latex] is base [latex]D=4[/latex], which is the size of the alphabet. A protein complexity score can be computed in an analogous fashion using base [latex]20[/latex] for amino acids. The factor of [latex]\frac{1}{N}[/latex], where [latex]N[/latex] is the number of characters in the sequence, is to ensure the value is between [latex]0[/latex] and [latex]1[/latex].
There is a program called [latex]\texttt{dust}[/latex] (R. Tatusov and D.J. Lipman unpublished) that can mask sequences of low complexity. It can be run by specifying the sequence and a threshold.
$ dust sequences.fasta 30
Here we are specifying a threshold of [latex]30[/latex], where the default is [latex]20[/latex]. Clearly, [latex]\texttt{dust}[/latex] is specifying a complexity score different from WF complexity because it can be greater than [latex]1[/latex].
2.4.2 Weight Matrices
Weight matrices are the most general representation of a motif. It is a probabilistic model that we will see can be used to compute the log-likelihood of a string being an instance of the motif compared to a “background” model.
Probabilistic Models of Motifs
The concept of the Position Specific Scoring Matrix (PSSM), also known as a weight matrix, was developed by Stormo et al [14].
Let’s begin by first by defining what isn’t a motif, using what is called a background model. A background model is a probabilistic representation of what a typical sequence looks like. The simplest background model is defined by single nucleotide probabilities [latex]p_A, p_C, p_G, p_T[/latex]. Under such a model, the probability of a sequence is computed as the product of the individual frequencies in the sequence. This can be expressed as
[latex]\label{bgModel} P(x|R) = \prod_{i=1}^{|x|} p_{x[I]}[/latex]
(2.2)
Consider the nucleotide frequencies [latex]\{p_b\}[/latex] for the human genome. These frequencies vary from position to position, and from chromosome to chromosome. Moreover, these frequencies will vary when comparing the promoters of genes and intergenic regions.
Our motif can be described by a matrix of probabilities [latex]f_{i,b}[/latex]. For a motif of length [latex]K[/latex], we have a matrix like:
[latex]f = \left( \begin{array}{ccccc} f_{1A} & f_{1C} & f_{1G} & f_{1T} \\ f_{2A} & f_{2C} & f_{2G} & f_{2T} \\ f_{3A} & f_{3C} & f_{3G} & f_{3T} \\ \cdots & \cdots & \cdots & \cdots \\ f_{KA} & f_{KC} & f_{KG} & f_{KT} \\ \end{array} \right)[/latex]
With this matrix, we can compute the probability (likelihood) of the sequence [latex]x[/latex] given that it is an instance of the motif [latex]M[/latex] by
[latex]\label{motifModel} P(x|M) = \prod_{i=1}^{K} f_{i, x[I]}[/latex]
(2.3)
Entropy and Information Content
One helpful way of describing such a model is the Shannon entropy [15]. Shannon entropy is a measure of the uncertainty of a model, in the sense of how unpredictable a sequence generated from such a model would be. For the single-nucleotide background model, the entropy is
[latex]H = - \sum_{b=A}^T p_b \log_2 p_b[/latex]
Note that while Shannon entropy is typically denoted H, this is not to be confused with enthalpy, which is also represented with H. The entropy is maximized when each nucleotide is equally likely, that is if [latex]p_b = \frac{1}{4}[/latex] for all [latex]b \in \{A,C,G,T\}[/latex]. It is intuitive that such a model would have the highest uncertainty, for example, compared to a model where [latex]p_A = 0.9[/latex] and all other frequencies very low. Therefore, the maximum entropy of our background model is:
[latex]H_{max} = - \left( \frac{1}{4} \log_2 \left( \frac{1}{4} \right) + \frac{1}{4} \log_2 \left( \frac{1}{4} \right) + \frac{1}{4} \log_2 \left( \frac{1}{4} \right) + \frac{1}{4} \log_2 \left( \frac{1}{4} \right) \right)[/latex]
Since [latex]\log_2 \frac{1}{4} = -2[/latex], we have
[latex]H_{max} = 2[/latex]
When the logarithms are base [latex]2[/latex], the units for such a quantity are called “bits,” as is with BLAST scores (See Section 3.3). When using natural logs, the units are “nits”. We can think of this value of [latex]2[/latex] bits as the information content associated with knowing a particular nucleotide. A bit of information can also be understood as the number of questions necessary to unambiguously determine an unknown nucleotide. You could ask, “Is it a purine?” If the answer is “no”, you could then ask is it [latex]C[/latex]? The answer to the second question always guarantees, non-canonical nucleotides aside, the nucleotide’s identity.
We can then compute the entropy at each position [latex]i[/latex] of our motif’s probability matrix by the expression
[latex]H_i =-\sum_{b=A}^T f_{i,b} \log_2 f_{i,b}[/latex]
The Information Content of a motif at each position can be defined as the reduction in entropy. That is, the the motif provides information inasmuch as it reduces the uncertainty compared to the background model. If the change in entropy is [latex]\Delta H_i = H_i - H_{max}[/latex], then the information content at position [latex]i[/latex] is
[latex]R_i =-Δ H= H_{max} - H_i[/latex]
Exercise 7
What is the entropy of a set of sequences with the nucleotide frequencies given by [latex]p_A = p_T = 0.3[/latex] and [latex]p_C = p_G = 0.2[/latex]?
2.4.3 Relative Entropy
Another useful concept for quantifying the information in a motif is the “relative entropy”, which is also known as the Kullback-Leibler divergence and as “information gain” [16]. For biological motifs, the expression for relative entropy at a particular position [latex]i[/latex] is defined by the equation
[latex]{D(f_i||p) = \sum_{b=A}^{T} f_{ib} \log \left(\frac{f_{ib}}{p_b}\right)}[/latex]
(2.4)
This expression quantifies how different two discrete probability distributions are, in this case the background frequencies [latex]p_b[/latex] and one position of our motifs’s probability matrix [latex]f_{ib}[/latex]
2.4.4 Building a Weight Matrix
A weight matrix can be built or defined when one has a collection of sequences that are determined to be instances of the motif. It is essential that the motif’s instances be precisely aligned, usually without gaps, such that each position of each sequence corresponds to the same position of the motif. Consider a set of sequences [latex]S = \{ x_1, x_2, x_3, ..., x_{N}\}[/latex]. We consider that each sequence [latex]x_j[/latex] corresponds to an instances of our motif. For example, the following are instances of the binding site for the Drosophila transcription factor Giant:
[latex]\begin{array}{ccc} x_1 &=& TTTATGTGAT\\ x_2 &=& GTTACGCAAT \\ x_3 &=& TTAATATAAC \\ x_4 &=& GTTACATAAT\\ x_5 &=& CCGGCGTATT\\ \cdots & & \\ x_N &=& GTTACGTAAT\\ \end{array}[/latex]
One useful contract is the Kronecker delta function. For this application, consider the expression [latex]\delta_{a,b}[/latex], which returns [latex]1[/latex] when [latex]a=b[/latex], and [latex]0[/latex] otherwise. For example, we can check if a particular nucleotide [latex]i[/latex] in sequence [latex]j[/latex] is equal to the nucleotide [latex]b[/latex] with the statement [latex]\delta_{b,x_j[i]}[/latex]. Under this representation, this function is defined as:
[latex]\begin{aligned} \delta_{b,x_j[i]} = \begin{cases} 1 & \mbox{if } x_j[i] = b\\ 0 & \mbox{if } x_j[i] \ne b\\ \end{cases} \end{aligned} \label{indicatorFunction}[/latex]
(2.5)
This function is useful for connecting sequences to equations. For example, we can generate a matrix of counts [latex]C[/latex], such that the elements [latex]C_{ib}[/latex] contain the number of occurrences of nucleotide [latex]b[/latex] at position [latex]i[/latex] in instances of our motif:
[latex]{C_{ib}=\sum_{j=1}^N\delta_{b,x_j[I]}}[/latex]
This count matrix can then be normalized to represent the frequency of each nucleotide at each position by
[latex]{f_{ib}=\frac{C_{ib}}{\sum_{b'=A}^T C_{ib'}}}[/latex]
Then, using equations 2.2 and 2.3 we can define a score as the log likelihood ratio of the probabilities of being an instance of the motif to being a random sequence. The expression of this score for a particular sequence [latex]x_j[/latex] is
[latex]{S(x_j) = \log \left( \frac{P(x|M)}{P(x|R)} \right) = \sum_{i=1}^{K} \log \left( \frac{f_{i x_j[i]}}{p_{x_j[i]}} \right)}[/latex]
As another example of the utility of the indicator matrix, this score can be represented as
[latex]{S(x_j) = \sum_{i=1}^{K} \delta_{b,x_j[i]} \log \left( \frac{f_{ib}}{p_{b}} \right) = \sum_{i=1}^{\ell} \sum_{b=A}^T \delta_{b,x_j[i]} W_{ib}}[/latex]
In the second part of the equation, we have defined the weight matrix [latex]W[/latex] with terms given by
[latex]{W_{ib} = \log \left( \frac{f_{ib}}{p_{b}} \right)}[/latex]
So, for a particular sequence, [latex]x_j = CGTAAGGT[/latex], this equation would pick out the appropriate terms necessary to compute the score
[latex]{S(x_j) = W_{1C} + W_{2G} + W_{3T} + W_{4A} + W_{5A} + W_{6G} + W_{7G} + W_{8T}}[/latex]
Note that for this score to make sense, you need to test a sequence [latex]x_j[/latex] that is the same length as the motif.
2.4.5 Biopython Motifs
The [latex]\texttt{motifs}[/latex] module
Now let’s see how we can go about building a weight matrix using Biopython [17]. First, we’ll need to import modules as usual. Next, we’ll need to specify a set of instances of our motif. In theory, this would be best done as reading in a FASTA file of instances. Next, we can create our motif from the list of instances. Here’s how this looks:
>>> from Bio import motifs
>>> from Bio.Seq import Seq
>>> instances = [Seq("CAGTT"),Seq("CATTT"),Seq("ATTA"),Seq("CAGTA"),Seq("CAGTT"),Seq("CAGTA")]
>>> motif = motifs.create(instances)
>>> print(motif.degenerate_consensus)
CAKTW
In this example, we have created a motif from a simple list of instances, each of which are [latex]\texttt{Seq}[/latex] objects, typed in using the [latex]\texttt{motifs.create()}[/latex] method. The method [latex]\texttt{degenerate\_consensus}[/latex] is useful for creating a concise sequence representation. We lose some information by only keeping this consensus sequence, and not keeping the matrix. By creating this motif object, we can also print out the count matrix for this motif:
>>> print(motif.counts)
0 1 2 3
A: 0.00 0.00 3.00 0.00
C: 6.00 0.00 0.00 2.00
G: 0.00 6.00 3.00 2.00
T: 0.00 0.00 0.00 2.00
JASPAR sites
We often want to create a motif from external data sources. One such database of motifs is JASPAR http://jaspar.genereg.net [18]. On this webpage we can browse through various motifs. For example, in the “JASPAR CORE Insecta” section, we can see the motif MA0447.1 for the Giant binding motif http://jaspar.genereg.net/cgi-bin/jaspar_db.pl?ID=MA0447.1&rm=present&collection=CORE. After downloading the “sites” file as a FASTA file in the lower left, we can see from the file “MA0447.1.sites” that it is similar to FASTA, but contains some additional information:
>MA0447.1 gt 1
tttctgttttggcgtaTTTATGTGATgc
>MA0447.1 gt 2
ggtggcactaccctGTTACGCAATat
>MA0447.1 gt 3
tTTAATATAACgcttctatctttgttta
>MA0447.1 gt 4
gttgttacgcgtGTTACATAATgcttcg
>MA0447.1 gt 5
aaccactgtaaagctCCGGCGTATTggc
...
We can see that there is additional information encoded in the capitalized letters, indicating where the binding site is. Secondly, this format doesn’t work for most programs as a FASTA file because the string directly after the “[latex]\gt[/latex]” not unique for each line, but instead the unique information comes after with the numbering. We therefore need a special method to read in this information. The [latex]\texttt{motifs}[/latex] module has a method for reading this information. Let’s create a logo while we’re at it:
>>> from Bio import motifs
>>> motif = motifs.read(open("MA0447.1.sites"),"sites")
>>> print(motif.counts)
0 1 2 3 4 5 6 7 8 9
A: 9.00 0.00 1.00 29.00 0.00 5.00 0.00 30.00 33.00 0.00
C: 4.00 1.00 0.00 0.00 29.00 0.00 3.00 2.00 1.00 8.00
G: 18.00 1.00 2.00 4.00 0.00 30.00 1.00 1.00 0.00 4.00
T: 4.00 33.00 32.00 2.00 6.00 0.00 31.00 2.00 1.00 23.00
>>> motif.weblogo("giant_LOGO.pdf",format="pdf")
This last command produces a LOGO image and requires an internet connection. It actually sends the data to the website http://weblogo.berkeley.edu/ [19]. The resulting LOGO image looks like this, which is similar to the motif logo seen on the JASPAR database:
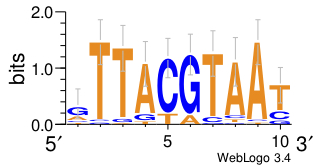
We’ve already seen how to score a particular sequence with a weight matrix, and how to build a weight matrix form a collection of instances. In practice, we often have longer sequences where we don’t know precisely where the instances are, but know that the sequences contain subsequences that are instances of the motif.
2.5 Promoters
Broadly speaking, the promoter of a gene is the set of genomic DNA sequences that direct the gene’s transcription. This can include the core promoter that is the most proximal region around the gene’s transcription start site, and can also include other regions of genomic DNA that are involved in transcription initiation.
2.5.1 Core Promoters
The core promoter is a collection of binding sites, capable of directing the initiation of transcription, and located within [latex]+/- 40bp[/latex] from the TSS. In eukaryotes, this can include the TATA-box and the Initiator, as well as other motifs that are more organism-specific.
2.5.2 Databases of Promoters/TSSs
There are a number of databases that are devoted to cataloging the locations of the promoters and transcription start sites of genes.
EPD: Eukaryotic Promoter Database
The Eukaryotic Promoter Database (EPD) is a resource of experimentally validated promoter locations for animals, plants, and fungi. This database contains non-redundant entries of promoter locations for Humans, mouse, D. melanogaster, zebrafish, C. elegans, Arabidopsis thaliana, S. cerevisiae, and S. pombe. The database can be accessed at http://epd.vital-it.ch/.
2.6 De novo Motif Finding
2.6.1 Gibbs Sampling
Gibbs sampling has many applications in statistical physics in general [20]. Is sometimes called a Markov-chain Monte Carlo (MCMC) approach. Briefly, Gibbs sampling starts with a set of sequences in which there is a motif of unknown sequence content. First, random initial positions of the motif are selected. Next, a weight matrix is built from those instances. The weight matrix is then used to re-score the positions of the input sequences, to find a new optimal set of instances, and the weight matrix is subsequently updated. This process is repeated until convergence. Perhaps surprisingly, this method is capable of finding motifs quite well.
You might try as a challenge exercise, to implement Gibb’s Sampling with Biopython. For example, if you have a list of sequences [latex]\texttt{seqs}[/latex], you can generate random positions for the initial motif instances for [latex]K=7[/latex] using the python module [latex]\texttt{random}[/latex], and extract subsequences corresponding to these positions.
>>> from Bio.Seq import Seq
>>> import random
>>> seqs = [Seq('GTCGATCGATCGTACGTACGTACGTACGATGCTAGCTACGTACC'),
Seq('GGTTCGAGTCGAGCAAGAGCTAGCTAGCGACGTACTAC'),
Seq('GCTGATCATGCTAGCGCGTAGCTACGATCGTACGTACGATGAGCTAGCTACGTCTACGTACGTGCACA')]
>>> K = 7
>>> instances = []
>>> for seq in seqs:
... instances.append(seq[j:j+K])
...
>>> print(instances)
[Seq('CGTACGT', Alphabet()), Seq('AAGAGCT', Alphabet()), Seq('CGCGTAG', Alphabet())]
You could create a motif from the instances as before. This will serve as the initial motif, and it would be updated repeatedly for some number of steps.
>>> from Bio import motifs
>>> motif = motifs.create(instances)
>>> print(motif.counts)
0 1 2 3 4 5 6
A: 1.00 1.00 0.00 2.00 0.00 1.00 0.00
C: 2.00 0.00 1.00 0.00 1.00 1.00 0.00
G: 0.00 2.00 1.00 1.00 1.00 1.00 1.00
T: 0.00 0.00 1.00 0.00 1.00 0.00 2.00
>>> weightMatrix = motif.pssm
>>> print(weightMatrix)
0 1 2 3 4 5 6
C: 1.42 -inf 0.42 -inf 0.42 0.42 -inf
G: -inf 1.42 0.42 0.42 0.42 0.42 0.42
T: -inf -inf 0.42 -inf 0.42 -inf 1.42
This weight matrix could in theory be used to collect the instances of the motif, and you could collect the top scoring instances for each of the input sequences, using something like this for each of the input sequences:
>>> for position,score in weightMatrix.search(seq):
... print(position, score)
These updated instances could be used to create new motif, and this process could be repeated. I leave this as a challenge for the reader
2.6.2 MEME and the EM Algorithm
One of the most widely used software tools for motif discovery is MEME: Multiple EM for Motif Elicitation. MEME uses Expectation Maximization to find the best binding sites [21]. The algorithm computes the parameters that maximize the expected value of the (log-)likelihood pf the model. The EM algorithm attempts to learn the “missing data”, in this case the positions of the instances of the motif. Once the instances of the motif are identified, an updated weight matrix can be computed.
MEME starts with some initialization of motifs built from the enriched K-mers. Essentially this list of initial motifs is achieved through a heuristic method, which applies one iteration of EM on all K-mers. The algorithm computes an expression for the expected value of the log-likelihood. It then computes the value of the motif membership variable Z that maximizes the expected value of the log-likelihood. This process is repeated until convergence.
There are numerous options for running MEME. For example, one can select how the instances of the motifs are distributed in the input sequences. They are specified by the “-mod” option and can be:
- oops – Exactly one instance per sequence.
- zoops – One or zero instances per sequence.
- anr – Any number of instances per sequence.
To find a motif in the input file “sequences.fa” that has a maximum motif length (specified with the -maxw option) and requiring exactly one occurence per sequence, we would use the following command
$ meme sequences.fa -dna -mod oops -maxw 12
Similarly, to find [latex]2[/latex] different motifs, each with a maximum length (width) of [latex]10[/latex], and such that each sequence has zero or one instance, we would use the following command:
$ meme sequences.fa -dna -mod zoops -maxw 10 -nmotifs 2
For a full list of options, try typing [latex]\texttt{meme --help}[/latex] on the command line.
2.7 Lab 3: Introduction to Motifs
In this lab, we are going to learn about various ways to produce motifs from sequence data. The purpose is to show what works and what doesn’t. Let’s start by creating a directory called [latex]\texttt{Lab3}[/latex], and [latex]\texttt{cd}[/latex] into this directory, similarly as before.
2.7.1 Part 1: Building a motif and LOGO image
First, let’s download a list of sequences that contain a motif at random positions and and some flanking sequence.
$ wget http://hendrixlab.cgrb.oregonstate.edu/teaching/gt.fasta
How many lines are in this file? How many sequences does that mean are in the file?
Let’s try and create a motif from this data. What do you expect to happen?
>>> from Bio import SeqIO
>>> from Bio import motifs
>>> from Bio.Seq import Seq
>>> sequences = SeqIO.parse("gt.fasta","fasta")
>>> instances = []
>>> for data in sequences:
... instance = data.seq
... instances.append(instance)
...
>>> motif = motifs.create(instances)
Now the motif is created in the “motif” object. What does the count matrix look like? You can print it out by this command:
>>> print(motif.counts)
Create a motif LOGO from these counts. We can go through the web, or we can create one right now with Biopython:
>>> motif.weblogo("giant_1.pdf",format="pdf")
>>> quit()
Does this look like a good motif? How can you tell?
2.7.2 Part 2: JASPAR Database and “sites” format.
Now go to the website JASPAR at http://jaspar.genereg.net. Go to “JASPAR CORE Insecta”. Then find the motif for “giant”, labeled “gt” (motif ID MA0447.1). Click the motif LOGO image to get a pop-up of the motif details (you may need to enable pop-ups on your browser). How does the motif LOGO compare to what we found just by building a LOGO from the FASTA file of all the sites? (If you have issues downloading the file, you can get it here.)
Now let’s download the sites in JASPAR format, which is a variation on FASTA, with a little more information. Click the link that says “(Show me all binding sites)..as fasta file” in the lower left portion of the pop-up. Transfer the downloaded file to crick by using the folder icon for file transfer. By looking at the file, what differences do you see?
$ less MA0447.1.sites
Now, let’s load this data using a special function that is part of the motifs module:
>>> from Bio import motifs
>>> motif = motifs.read(open("MA0447.1.sites"),"sites")
>>> print(motif.counts)
How does this compare to what you found previously? Now create a motif LOGO and exit:
>>> motif.weblogo("giant_2.pdf",format="pdf")
>>> quit()
How does this motif compare to the image on the JASPAR webpage
2.7.3 Part 3: Running MEME on the command line
The reason why our first method didn’t work is because we just looked at sequences without performing motif finding. The JASPAR sites file encodes this information in the capital letters, letting it know where the motif instances are. Now let’s try motif finding on the first set of data to see if we can recover it.
$ meme gt.fasta -dna -mod oops -nmotifs 1 -maxw 12 -o gt_3
What do each of these parameters mean? Take a look at the output file. Note the “information content” information, as well as probability scores (p-values) for the instances.
$ less gt_3/meme.txt
Finally, by using the file transfer icon, let’s look at the meme.html output file and associated LOGO image generated by MEME. How does this compare to the actual motif in JASPAR?
Bonus question: What happens when you add the “-revcomp” flag to MEME? What is the difference in the output and why do you think this is?
$ meme gt.fasta -dna -revcomp -mod oops -nmotifs 1 -maxw 12 -o gt_4

