Public-Key Cryptography
What You’ll Learn
- The difference between symmetric- and asymmetric-key cryptography
- How public-key cryptography works
Encryption protocols can be classified into two major types. In symmetric-key cryptography, the key used to decrypt a message is the same as (or easy to transform from) the key used to encrypt the message. This is the case for the basic ciphers (Caesar, Vigenère, and the onetime pad) that we described in the chapter “What Is Encryption?” (There are, of course, modern symmetric-key ciphers that are used—for example, to encrypt the data on your phone or computer.) As we saw, these protocols are challenging to use for communication because you need to first find some way to privately share the key with your communication partner. Diffie-Hellman key exchange gave a method for two people to generate a shared key (that can be used in a symmetric-key encryption protocol) while only communicating over an insecure channel (such as the internet).
Asymmetric-key cryptography or public-key cryptography solves the key sharing problem in a different way. Rather than have one key that is used to both encrypt and decrypt, public-key cryptography uses two keys: one key to encrypt (called the public key) and one key to decrypt (called the private key). This pair of keys has the following properties:
- It is infeasible to generate the private key from the public key: the keys must be generated together.
- A message that is encrypted by the public key can only be (feasibly) decrypted with the corresponding private key.
Suppose Bobby wants to send Assata an encrypted message. Assata creates a private-key/public-key pair and sends Bobby her public key (over an insecure channel). Bobby uses the public key to create the ciphertext and sends the ciphertext to Assata. The ciphertext can only be decrypted using Assata’s private key. Even though anyone may have Assata’s public key, the only thing that can be done with the public key is encrypt messages that can only be decrypted using Assata’s private key. Security is therefore achieved by keeping the private key private: secret and secure.
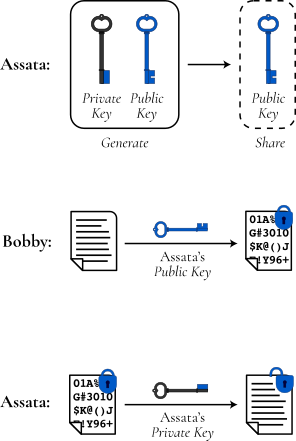
In this model, anyone can, in fact, publish their public key. For example, Assata could publish her public key online so that anyone wishing to send Assata an encrypted message could encrypt that message with her public key first. Likewise, Bobby could create his own pair of public and private keys and publish his public key online so that others could send him encrypted messages that only Bobby could decrypt with his (securely stored) private key.
Revisiting Diffie-Hellman Key Exchange: Public-Key or Symmetric-Key Cryptography?
Let’s revisit Diffie-Hellman key exchange through the lens of symmetric and public-key cryptography. Recall that Assata and Bobby agree (publicly/insecurely) on a number p. Assata picks a (secret) number a and computes p ☆ a to send (publicly/insecurely) to Bobby. One could thus view a as Assata’s private key, p ☆ a as Assata’s public key, and this scheme as part of a public-key protocol. But Bobby picks his own secret number b and combines it with Assata’s public key to get p ☆ a ☆ b. Likewise, Assata combines Bobby’s “public key” p ☆ b with her own private key to get p ☆ b ☆ a. Since p ☆ a ☆ b = p ☆ b ☆ a, Assata and Bobby have a common key to use for encryption, and they use the same key for decryption. In this way, this is part of a symmetric-key protocol. For these reasons, the Diffie-Hellman key exchange lies somewhere between public-key and symmetric-key cryptography.
Combining Public-Key and Symmetric-Key Cryptography
Public-key encryption is usually more computationally expensive than symmetric-key encryption. To achieve the same security guarantees (e.g., against brute force and other attacks), public keys need to be much longer than symmetric keys. Also, performing the encryption itself takes longer using public keys than symmetric keys. There is also the problem that the longer you use a key for encryption, the more ciphertext examples there are to try to use to break the encryption (other than brute force)—that is, keys tend to age poorly.
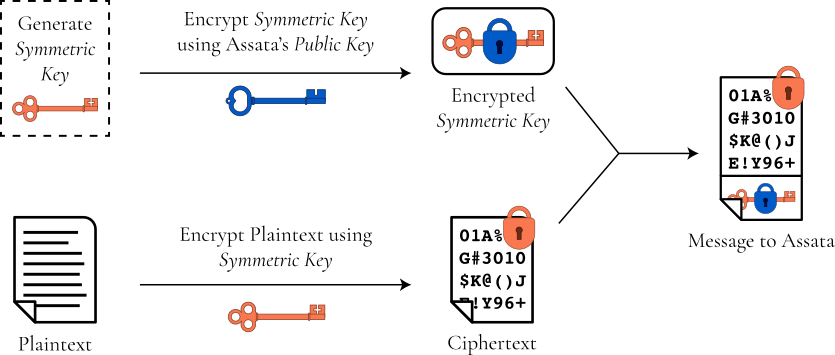
For these reasons, public keys are generally used to encrypt a symmetric key for a given (communication) session. Suppose Bobby wishes to send Assata an encrypted message. Bobby generates a symmetric encryption key and encrypts the message with the symmetric key using a symmetric cipher. He then encrypts the symmetric key using Assata’s public key. He sends the encrypted message and the encrypted key to Assata:
Assata decrypts the encrypted key using her private key and then uses the result to decrypt the encrypted message:
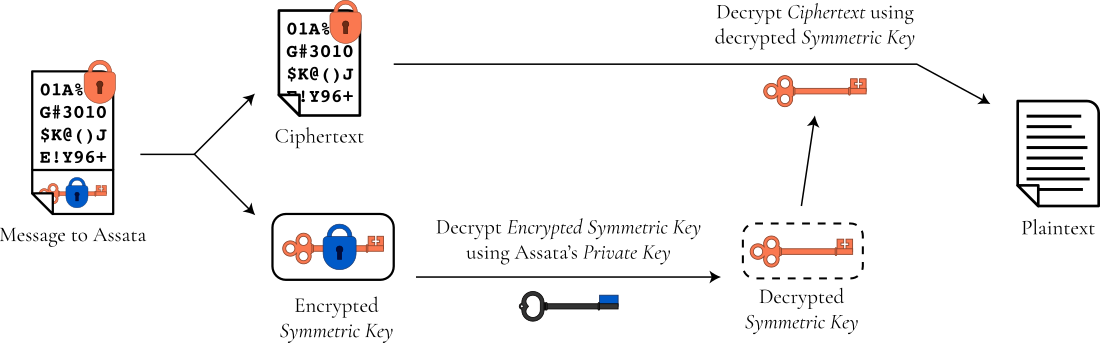
Since the public key is only used to encrypt keys (which are typically random-looking strings), the public key does not age, because methods of breaking the encryption that rely on human-language phrases would fail. An added benefit is that if one message is successfully decrypted, that does not help in breaking the encryption of a different message, since each message is encrypted with a different key.
In Context: Antinuclear Activism and Pretty Good Privacy
A particularly robust implementation of public-key cryptography is PGP, an acronym for the understatement Pretty Good Privacy. (An interoperable, free, and open-source version of PGP is GPG, or GNU Privacy Guard.) PGP encryption is most commonly used for encrypting email communications with several plug-ins and email clients that support using PGP encryption. There are a number of (synchronized) online directories of PGP keys, each associated with an email address, that allow Bobby to look up Assata’s PGP key in order to send her an encrypted email.
Phil Zimmermann, a longtime antinuclear activist, created PGP in 1991 so similarly inclined people might securely use bulletin-board services (BBSes, the Reddit of the 1980s) and securely store messages. He developed PGP as an open-source project, and no license was required for its noncommercial use. Posting it initially to a newsgroup that specialized in grassroots political organizations, mainly in the peace movement, PGP made its way to a newsgroup used to distribute source code and quickly found its way outside the United States. Users and supporters included dissidents in totalitarian countries, civil libertarians, and cypherpunks. However, at the time, cryptosystems using keys larger than forty bits were then considered munitions within the definition of the US export regulations. PGP was initially designed to support 128-bit keys. In February 1993, Zimmermann became the formal target of a criminal investigation by the US government for “munitions export without a license.” Zimmermann challenged this by publishing the entire source code of PGP in a book, which was distributed and sold widely. Anybody wishing to build their own copy of PGP could cut off the covers, separate the pages, and scan them using an OCR program, creating a set of source code text files. While the export of munitions (guns, bombs, planes, and software) was (and remains) restricted, the export of books is protected by the First Amendment. After several years, the investigation of Zimmermann was closed without filing criminal charges against him or anyone else.
US export regulations regarding cryptography remain in force but were liberalized substantially throughout the late 1990s. PGP encryption no longer meets the definition of a nonexportable weapon.
What to Learn Next
External Resources
- Electronic Frontier Foundation. “A Deep Dive on End-to-End Encryption: How Do Public Key Encryption Systems Work?” Surveillance Self-Defense, September 29, 2014.
- Zimmermann, Phil. “Why I Wrote PGP.” 1999.
Media Attributions
- pubkeycrypto-key-gen-share © OSU OERU is licensed under a CC BY-NC (Attribution NonCommercial) license
- pubkeycrypto-split1-encrypt © OSU OERU is licensed under a CC BY-NC (Attribution NonCommercial) license
- pubkeycrypto-split2-decrypt © OSU OERU is licensed under a CC BY-NC (Attribution NonCommercial) license

